Five cards are dealt from a standard 52-card deck. What is the probability of drawing four face cards and an Ace? First, we do it analytically.
Combinations
We are choosing four face cards from the total possible 12 (and without replacement). Since the order of the deal doesn’t matter, it is a combination problem of the following form.
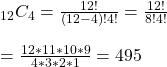
Now, calculate the ways of choosing one ace card from a total of four.
![]()
To get the required probability, we have to divide the product of the two with all the possible combinations (of selecting five cards from the deck of 52).
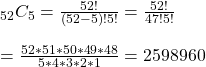
Finally, the probability is calculated by dividing the combination of getting four face cards and one ace card with the possibility of getting five cards from the deck.
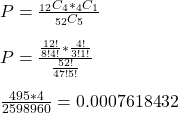
We can execute the whole calculation using the following R code:
choose(12,4)*choose(4,1)/choose(52,5)Monte Carlo
Let’s start building the deck as we did last time.
suits <- c("Diamonds", "Spades", "Hearts", "Clubs")
face <- c("Jack", "Queen", "King")
numb <- c("Deuce", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine", "Ten")
face_card <- expand.grid(Face = face, Suit = suits)
face_card <- paste(face_card$Face, face_card$Suit)
numb_card <- expand.grid(Numb = numb, Suit = suits)
numb_card <- paste(numb_card$Numb, numb_card$Suit)
Aces <- paste("Ace", suits)
deck <- c(Aces, numb_card, face_card)Now start drawing five cards at random and check your hands. Repeat that a million times, and count the number of times you got what you wanted. And divide it by the million.
B <- 1000000
results <- replicate(B, {
hand <- sample(1:52, 5, replace = FALSE)
deal <- deck[hand]
match_1 <- sum(face_card %in% deal)
match_2 <- sum(Aces %in% deal)
if(match_1 == 4 & match_2 ==1) {
counter <- 1
}else{
counter <- 0
}
})
sum(results) / B 
