Another counterintuitive experience similar to Downs–Thomson’s is Braess’s Paradox. As per this phenomenon, adding more roads to an existing network can slow down the overall traffic. Similar to the previous, we will see the mathematical explanation first.
Suppose there are two routes to city B from city A, as shown in the picture – the top and bottom roads. The first part is narrow on the top road, followed by a broad highway. The situation is the opposite for the bottom road.
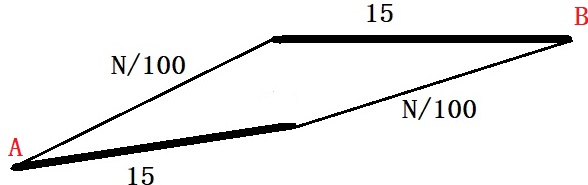
The highways are not impacted by the number of cars, whereas, for the narrower roads, the traffic time is related to the number of vehicles on the road – N/100, where N is the number of cars.
If there are 1000 cars in the city, the system will reach the Nash equilibrium by cars getting equally divided (in the longer term), i.e., 500 on each road. Therefore, each car to take
500/100 + 15 = 20 mins
Imagine a new interconnection built by the city to reduce traffic congestion. The travel time on the connection section is 1 minute. Let’s look at all scenarios.
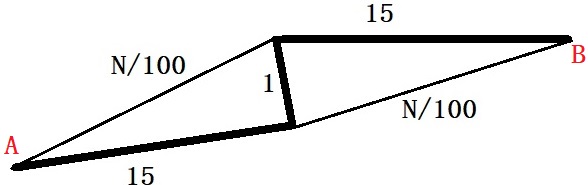
Scenario 1: A car starts from the bottom highway, takes the connection, and moves to the top highway. Total time = 15 + 1 + 15 = 31 mins.
Scenario 2: One car starts from the top road, takes the connection, and moves to the bottom road, while the others follow the old path (not using the connection). Total time = 50/100 + 1 + 51/100 ~ 11 mins.
Scenario 2 seems a no-brainer to the car driver. But this news invariably reaches everyone, and soon, everyone starts taking the narrow paths! In other words, the narrow route is the dominant strategy. The total travel time now becomes:
1000/100 + 1 + 1000/100 = 21 min. This is more than the old state, a situation with no connection possible.
So, the condition without the connection road (or closing down the connection road) seems a better choice. And this is Braess’s paradox suggesting that a more complex system may not necessarily be a better choice.

