A quick recap: in the previous post, we set a target of finding the bias of a coin by flipping it and collecting data. We have assumed a prior probability for the coin bias. Then established a likelihood for a coin that showed a head on a single flip.
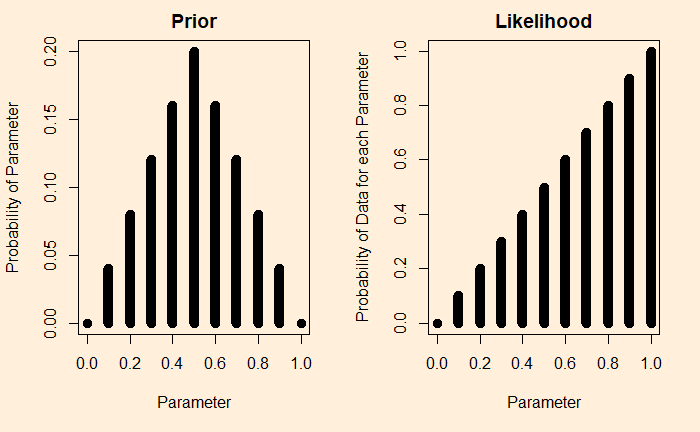
We know we can multiply prior with the likelihood and then divide by the probability of the data.
![]()
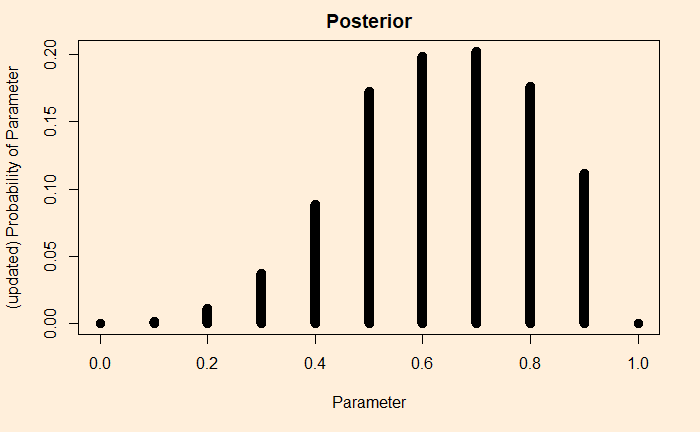
The outcome (posterior) is below.
Look at the prior and then the posterior. You see how one outcome (heads on one flip) makes a noticeable shift to the right. It is no more equally distributed to the left and the right.
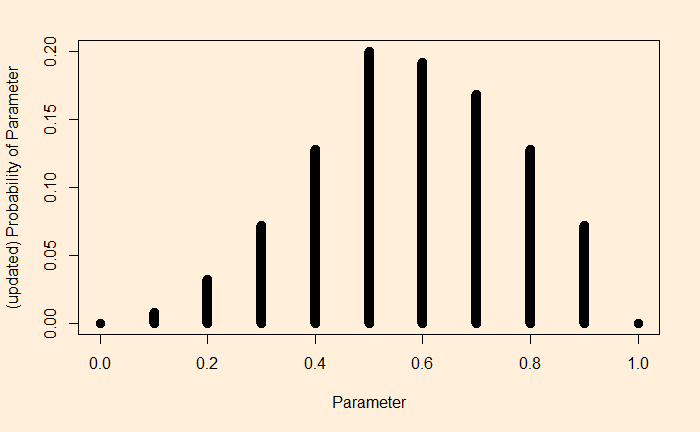
What would happen if, for the same prior, but getting two heads? First, calculate the likelihood:
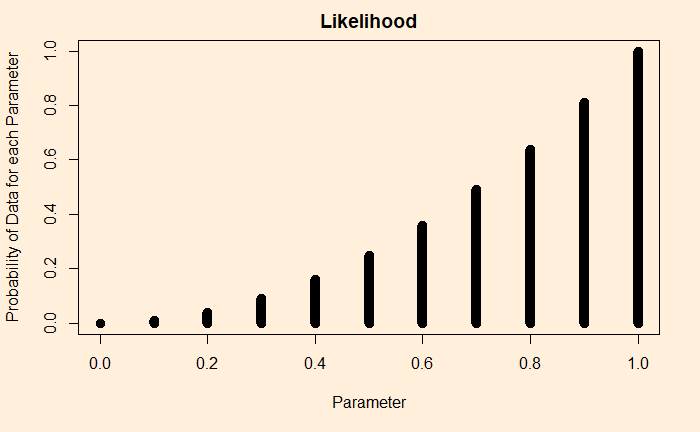
You can see a clear difference here as the appearances of the two heads changed the likelihood heavily to the right. The same goes for the updated chance (the posterior).