| Year | Accidents |
| 1976 | 24 |
| 1977 | 25 |
| 1978 | 31 |
| 1979 | 31 |
| 1980 | 22 |
| 1981 | 21 |
| 1982 | 26 |
| 1983 | 20 |
| 1984 | 16 |
| 1985 | 22 |
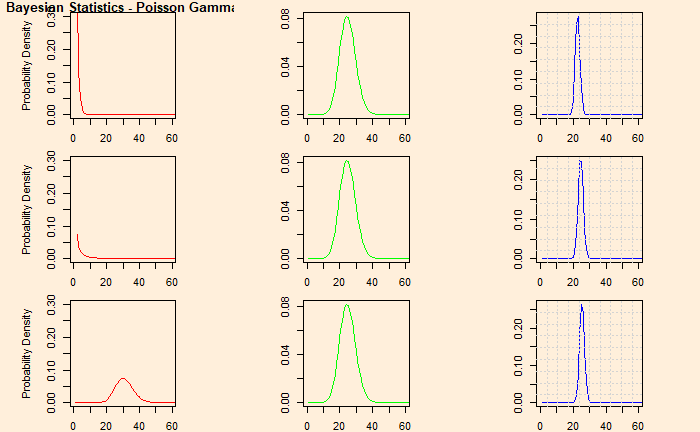
We assume that flight accidents are random and independent. This implies that the likelihood function (the nature of the phenomenon) is likely to follow a Poisson distribution. Let Y be the number of events occurring within the time interval.
![]()
Theta is the (unknown) parameter of interest, and y is the data (total of 10 observations). We will use Bayes’ theorem to estimate the posterior distribution p(theta|data) from a prior, p(theta). As we established long ago, we select gamma distribution for the prior (conjugate pair of Poisson).