Basics Continued

Continuing from the previous post, we will calculate a few more properties. We start with percentiles.

2	15	29	44	50	61	73
3	16	32	44	51	62	74
9	19	32	44	52	69	75
12	20	37	45	54	69	79
12	22	38	48	54	69	88
15	26	38	49	56	72	90
15	28	38	50	57	72	93

Percentiles

Percentile, P_x, is the value below which x percentage of the data lies. It is calculated as:

$P_x \approx \frac{x(n+1)}{100}$

For the problem described above, P₁₀ = 10 x 50 / 100 = 5, for n = 49. I have marked the fifth element of the table in bold (12). Similarly, P₉₀ = 90 x 50 / 100 = 45. The 45th element is 75.

quantile(machine, 0.1)
quantile(machine, 0.9)

Quartiles

Extending it further, we can get the quartiles as P₂₅ (first quartile, Q1), P₅₀ (second quartile, or median, Q2), and P₇₅ (third quartile, Q3). P₂₅ comes out to be (25 x 50 /100), the 12.5^th element. You either round it off to the nearest whole number (13) and select the 13^th number, which is 26 or take the 12^th number and add 0.5x(13^th – 12^th) = 22 + 0.5 x (26 – 22) = 24. Or 25% of the instruments will fail by 24 weeks. Similarly, P₇₅ = 37.5^th element = 69.

Inter-Quartile distance (IQD) is the difference between Q1 and Q3. Here, 69 – 26 = 43.

Variance

Variance is the measure of the variability of the data from the mean

$\text{population variance } = \frac{\sum\limits_{i = 1}^n(X_i - \mu)^2}{n}$

The square root of the variance is the well-known standard deviation.

$\sigma = \sqrt{\frac{\sum\limits_{i = 1}^n(X_i - \mu)^2}{n}}$

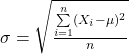
Note that the above equations are for the population. The corresponding entities for the sample are

$\\ \text{sample variance, } = \frac{\sum\limits_{i = 1}^n(X_i - \bar{X})^2}{n -1} \\ \\ \text{sample standard deviation }S = \sqrt{\frac{\sum\limits_{i = 1}^n(X_i - \bar{X})^2}{n -1}}$

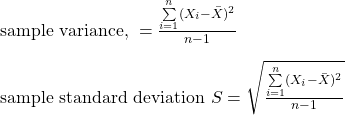
Chebyshev’s theorem

It is an empirical rule to predict the proportion of observations likely to lie between an interval defined using mean and standard deviation.

$P(\mu - k\sigma \le X \le \mu + k\sigma) \ge 1 - \frac{1}{k^2}$

For example, what proportion of data lies between two standard deviations? It is 1 – 1/22 = 0.75 or 75%. In our case, the mean is 44.94, and the standard deviation is 24.19. The interval is between [44.94 – 2 x 24.19] and [44.94 + 2x 24.19] or between -3.44 and 93.32. The number of data between these is everything or 100%! So Chebyshev gives an approximation lower than the exact. You may recall that for normally distributed data, two standard deviations cover about 95% of the data.

Percentiles

Quartiles

Variance

Chebyshev’s theorem

Related Posts