Back to basics

In the beginning, there was dice

Probability on the margins

dice, game, random-1963300.jpg

What is the probability of getting a 3 on a single roll of dice? You can calculate that by dividing the number of 3s by all possible numbers the die has.

123456

It is one 3 out of the possible six numbers, or (1/6). The probability of this type is called a marginal probability. The probability of one character of interest, say P(A). Or the one that is on the margins!

Two things at once

dice, die, cube-149215.jpg

You throw two dice – one green and one violet. What is the probability that you get a green 3? It is the joint probability of two outcomes – a colour and a number – at once. The notation is:

P(Green \displaystyle \cap 3)

The upside-down U is the symbol of intersection or AND.

Green 1Green 2Green 3Green 4Green 5Green 6
Violet 1Violet 2Violet 3Violet 4Violet 5Violet 6

Only one instance of Green 3 in a total of possible 12 outcomes, so the joint probability is (1/12). When you hear joint, imagine an upside-down U and think it meant AND. What about the opposite?

\\ P(3 \displaystyle \cap Green) \\ \\ \text{that is also (1/12). In other words,} \\ \\ P(3 \displaystyle \cap Green) = P(Green \displaystyle \cap 3)

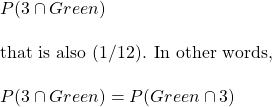
Two things, with a clue

Now, what is the probability of seeing a 3 given it is a Green? This is a conditional probability and is represented as:

P(3 | Green)

You don’t need another table to answer that. If green is known, then there is only 1 out of 6 chances for a 3 or (1/6). What about the opposite, P(Green|3)? It’s (1/2) because if 3 is known, the choices are only two: green or violet. So, remember, P(A|B) and P(B|A) are not equal.

Formalising

We will start with the definition of joint probability as we had seen in AND rule earlier.

\\ P(Green \displaystyle \cap 3) =P(3 | Green) \text{ x } P(Green) --- (1) \\ \\ \text{ OR} \\ \\ P(3 | Green) = \frac{P(Green \displaystyle \cap 3)}{P(Green)} \\ \\ \text{But} P(Green \displaystyle \cap 3) = P(3 \displaystyle \cap Green) \\ \\ \text{Appying the definition of} \displaystyle \cap \text{once again: on } P(3 \displaystyle \cap Green) \\ \\ P(3 | Green) = \frac{P(Green| 3) \text{ x } P(3)}{P(Green)} --- (2)

Does the last equation remind you of something? Yes, it is one form of Bayes’ equation.

Let’s verify with numbers: first, equation (1) P(Green AND 3) = P(3|Green) x P(Green) = (1/6)x(1/2) = (1/12). Equation (2) P(3|Green) = P(Green|3) x P(3)/ P(Green) = (1/2) x (1/6) / (1/2) = (1/6).

The dice example is simplistic because the descriptors Green and 3 are independent. It’s fun once we have more dependent probabilities. But then, we have seen many of them in the previous posts.

Bayes’ equation

Look at the equation again.

P(3 | Green) = \frac{P(Green| 3) \text{ x } P(3)}{P(Green)}

  1. The equation relates P(3|Green) with P(Green|3)
  2. The equation calculates P(3) from a known value of P(3)! Don’t you see P(3) on both sides? In case you don’t, P(3|Green) is, after all, P(3). The difference is that some additional information in the name of green is available to use. It is still about P(3) and not about P(Green). So to rephrase observation 2, the Bayes’ equation updates the knowledge of P(3) using additional information. That additional information comes from P(Green).

Related Posts