Asymmetric Coin-Toss Game

Here is another coin-tossing game. If it lands on heads, your money increases by 80%, and if it’s tails, it reduces by 50%. The question is: will you play this game?

As always, let’s estimate the expected value of this game.
E =0.8 x 0.5 – 0.5 x 0.5 = 0.4 – 0.25 = 0.15 or a net gain of 15%. In other words, if I start with $100 and bet everything each time 20 times, on average, I end up getting 100 x 1.15²⁰ = $1637.

Let 10,000 play this game and collect the average.

n_people <- 10000
n_bet <- 20
gain <- data.frame(matrix(NA, nrow = n_bet, ncol = n_people))
 
  for (m in 1:n_people) {
       bet1 <- 100
       money <- c(rep(0, n_bet))
       for (n in 1:n_bet) {
           bet2 <- bet1
           toss <- sample(c(0.8*bet2,-0.5*bet2), size = 1, replace = TRUE, prob = c(1/2,1/2))
           bet1 <- bet1 + toss
           money[n] <- bet1 
           gain[n,m] <- money[n]
       }
  }   
  gain$AVG <- apply(gain, 1, mean, na.rm=TRUE)

Yes, we get $1694.8 as the average of 10,000 people at the end of 20 rounds.

So, a no-brainer, huh? But before we make a decision, what is the median return from the game? In other words, what does the average person get: it’s 34.86!

gain$MED <- apply(gain, 1, median, na.rm=TRUE)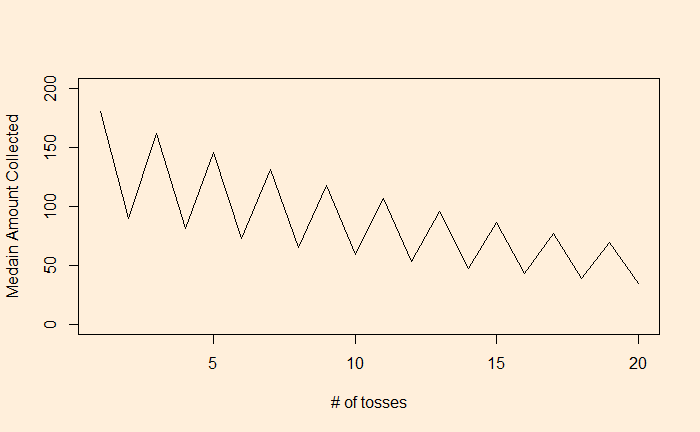

So, the average person systematically loses money.