Annie’s Table Game – Frequentist vs Bayesian 

See the story and numerical experiments in the previous post. Annie is currently leading 5-3; what is the probability that Becky will reach six and win the game?

Frequentist solution 

Based on the results so far, 3 wins in 8 matches, Beck’s probability of winning is (3/8). That means the probability of Becky winning the next three games (to reach 6 before Annie wins another, which will make her 6) is (3/8)3 = 0.053.

Bayesian solution 

First, we write down the Bayes equation. The probability of B winning the game, given A is leading 5-3, 

\\ P(B|A_{5-3}) = \frac{P(A_{5-3}|B)*P(B)}{P(A_{5-3})}

Let’s start with the denominator. If p represents the probability of Becky winning a game, the probability of a 3-5 or 3 in 8 result is obtained by applying the binomial equation. The denominator is the sum of all possible scenarios (p values from 0 to 1). In other words, The denominator is,

\\ P(A_{5-3}) = \int_0^1 _8C_3 p^3 (1-p)^5

We use an R shortcut to evaluate the integral as the area under the curve using the ‘AUC’ function from the ‘DescTools’ library.

library(DescTools)
x <- seq(0,1,0.01)
AUC(x, choose(8,3)*x^3*(1-x)^5, from = min(x, na.rm = TRUE), to = max(x, na.rm = TRUE)) 
0.1111

And here is the area. 

plot(x, choose(8,3)*x^3*(1-x)^5, type="l", col="blue", ylab = "")
polygon(x, choose(8,3)*x^3*(1-x)^5, col = "lightblue")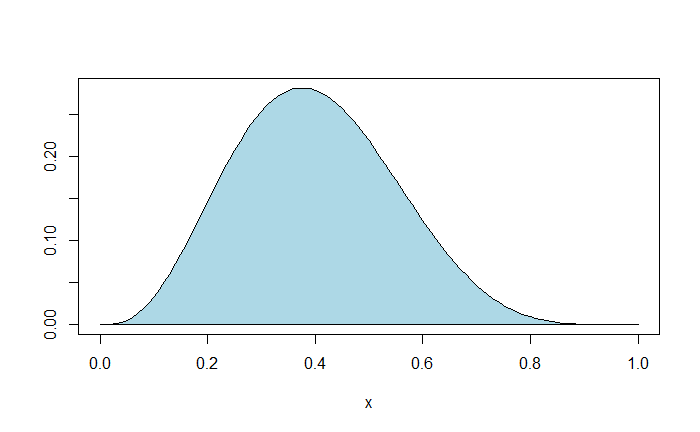

The numerator is the multiplication of the likelihood function with the prior probability of Becky winning three games. We will use a binomial equation as the prior function and p x p x p = p3 as P(B). 

\\ P(A_{5-3}|B)*P(B) = 8C_3 p^3 (1-p)^5 p^3 \\ \\ 8C_3 p^6 (1-p)^5

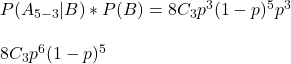
Again, the area under the curve all possible p values (0 -1), 

AUC(x, choose(8,3)*x^6*(1-x)^5, from = min(x, na.rm = TRUE), to = max(x, na.rm = TRUE)) 
0.0101

The required Bayesian posterior is 0.0101/0.1111 = 0.0909

To sum up

The Bayesian estimate is almost double compared to the frequentist. The Bayesian estimate is much closer to the results we saw earlier. Does this make Bayesian the true winner? We’ll see next. 

Related Posts