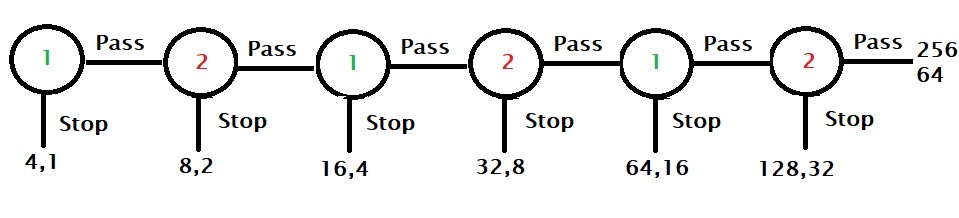
Here is a game played between two players, player 1 and player 2. There are two piles of cash, 4 and 1, on the table. Player 1 starts the game and has a chance to stop the game by taking four or the pass to the next player. In the next round, before player 2 starts, each stack of money is doubled, i.e. they become 8 and 2. Player 2 now has the chance to take a pile and stop or pass it back to player 1. The game continues for a maximum of six rounds.
Best strategy
To find the best strategy, we need to start from the end and move backwards. As you can see, the last chance is with player 2, and she has the option to end the game by taking 128 or else the other player will get 256, leaving 64 for her to take.
Since player 1 knows that player 2 will stop the game in the sixth round, he would like to end in round five, taking 64 and avoiding the 32 if the game moved to another.
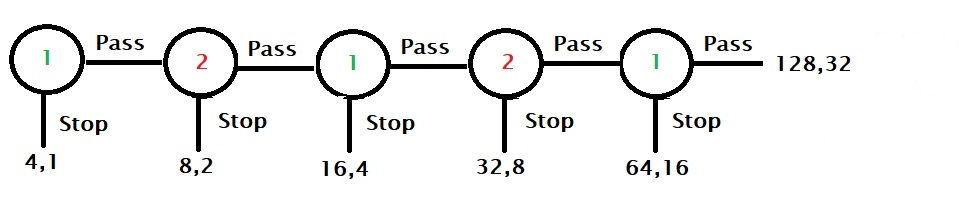
Player 2, who understands that there is an incentive to be the player who stops the game, can decide to stop earlier at fourth, and so on. So by applying backward induction, the rational player comes to the Nash equilibrium and controls the game in the first round, pocketing 4!
Irrationals earn more
On the other hand, player 1 passes the first round, signalling cooperation to the other player. Player 2 may interpret the call and let the game to the second round, trusting to bag the ultimate prize of 265. Here onwards, even if one of them decides to end the game, which is a bit of a letdown to the other, both players are better off than the original Nash equilibrium of 4.

