We know how to use a 1-sample t-test to perform a hypothesis test on the mean of a single group and a 2-sample t-test to compare two groups. The scope of t-tests ends here as two is the limit. What happens when you have three groups of data? If the number is two or more, you will use the analysis of variance or ANOVA. As we have done before, we will do an ANOVA using R programming.
Comparing four vendors
ANOVA requires an independent variable (categorical factor) and a dependent variable (continuous). The following table will tell you what I meant. The data used in the analysis is taken from https://statisticsbyjim.com/. The strength of certain materials from four vendors is available, and we are determining if there is a statistically significant difference between the mean strengths. Here is how a few selected entries appear (out of 40).
| Vendor | Strength |
| Vendor 1 | 11.71 |
| Vendor 1 | 11.981 |
| Vendor 1 | 8.043 |
| Vendor 2 | 7.77 |
| Vendor 2 | 10.74 |
| Vendor 2 | 10.72 |
| Vendor 3 | 9.65 |
| Vendor 3 | 8.79 |
| Vendor 3 | 10.86 |
| Vendor 4 | 6.97 |
| Vendor 4 | 9.16 |
| Vendor 4 | 8.67 |
Note that the categorical factor, vendor names (1, 2, 3 and 4), divided the continuous data into four groups. Before performing ANOVA, we plot the data and check how they look.
par(bg = "antiquewhite")
boxplot(AN_data$Strength ~ factor(AN_data$Vendor), xlab = "Vendor", ylab = "Strength of Material")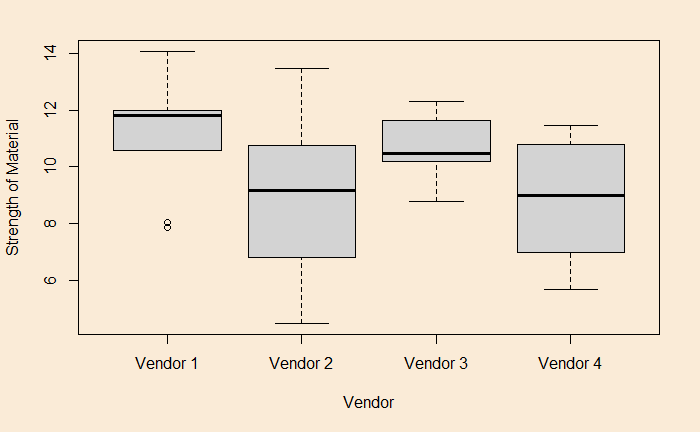
The null and alternate hypotheses are:
N0 = four mean strengths are equal
NA = four mean strengths are not equal
Doing ANOVA is pretty easy; the following commands will do the job.
sum_aov <- aov(AN_data$Strength ~ factor(AN_data$Vendor))
summary(sum_aov) Df Sum Sq Mean Sq F value Pr(>F)
factor(AN_data$Vendor) 3 43.62 14.540 3.303 0.0311 *
Residuals 36 158.47 4.402
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1We are testing the statistical significance by the F-test. And here is the most important thing, the p-value is 0.03, less than the 0.05 we chose. So the null hypothesis is rejected. We will see what they all mean, in the next post.
Hypothesis Testing: An Intuitive Guide: Jim Frost

