Card Games – Continued

Five cards are dealt from a standard 52-card deck. What is the probability of drawing four face cards and an Ace? First, we do it analytically.

Combinations

We are choosing four face cards from the total possible 12 (and without replacement). Since the order of the deal doesn’t matter, it is a combination problem of the following form.

\\ _{12}C_4 = \frac{12!}{(12-4)!4!} = \frac{12!}{8!4!} \\ \\ = \frac{12*11*10*9}{4*3*2*1} = 495

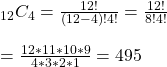
Now, calculate the ways of choosing one ace card from a total of four.

\\ _{4}C_1 = \frac{4!}{(4-1)!1!} = \frac{4!}{3!} = 4

To get the required probability, we have to divide the product of the two with all the possible combinations (of selecting five cards from the deck of 52).

\\ _{52}C_5 = \frac{52!}{(52-5)!5!} = \frac{52!}{47!5!} \\ \\ = \frac{52*51*50*49*48}{5*4*3*2*1} = 2598960

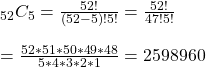
Finally, the probability is calculated by dividing the combination of getting four face cards and one ace card with the possibility of getting five cards from the deck.

\\ P = \frac{_{12}C_4 * _4C_1} {_{52}C_5} \\ \\ P = \frac{\frac{12!}{8!4!}*\frac{4!}{3!1!}}{\frac{52!}{47!5!}} \\ \\ \frac{495 * 4}{2598960} = 0.0007618432

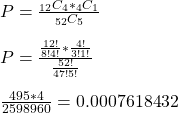
We can execute the whole calculation using the following R code: 

choose(12,4)*choose(4,1)/choose(52,5)

Monte Carlo

Let’s start building the deck as we did last time.

suits <- c("Diamonds", "Spades", "Hearts", "Clubs")
face <- c("Jack", "Queen", "King")
numb <- c("Deuce", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine", "Ten")

face_card <- expand.grid(Face = face, Suit = suits)
face_card <- paste(face_card$Face, face_card$Suit)

numb_card <- expand.grid(Numb = numb, Suit = suits)
numb_card <- paste(numb_card$Numb, numb_card$Suit)

Aces <- paste("Ace", suits) 

deck <- c(Aces, numb_card, face_card)

Now start drawing five cards at random and check your hands. Repeat that a million times, and count the number of times you got what you wanted. And divide it by the million.

B <- 1000000

results <- replicate(B, {

hand <- sample(1:52, 5, replace = FALSE)
deal <- deck[hand]

match_1 <- sum(face_card %in% deal)
match_2 <- sum(Aces %in% deal)

if(match_1 == 4 & match_2 ==1) {
  counter <- 1 
}else{
  counter <- 0
}
  
})

sum(results) / B

Related Posts