Chances of Rare Events

We have come across Poisson distribution a few times already. It is a way of estimating the probabilities of rare and independent events. But do you know Poisson is related to binomial distribution under certain circumstances?

But that should not come as a surprise. The binomial function estimates the probability of the number of successes in n discrete and independent trials, each with a chance of success = p. Whereas, Poisson gives the same but for rare events (events with low probabilities). In other words, Poisson is a special case of binomial when p is small ( p -> 0) and n is high (n -> infinity) (and its parameter lambda = n x p stays fixed). Let’s test this with an example.

A typist makes one mistake in every 500 words. If one page contains 300 words, what is the probability that she made no more than two mistakes in five pages?

Binomial

Start with Binomial for s occurrences in n trials.

\\ P(X = s) = nCs * p^s * (1-p)^{n-s} \\ \\ P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2) \\\\ P(X = 0) = 1500C0 * (1/500)^0 * (1-1/500)^{1500-0} = 0.0496 \\ \\ P(X = 0) = 1500C1 * (1/500)^1 * (1-1/500)^{1500-1} = 0.149\\ \\ P(X = 0) = 1500C2 * (1/500)^2 * (1-1/500)^{1500-2} = 0.224\\ \\ \text{sum all three terms, } \\\\ P(X \leq 2) = 0.423

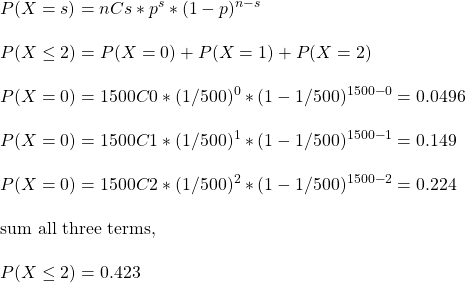
P(X = s) in the equation should be read as: “what is the probability that a random variable called X has a value s”.

Poisson

Since p = 1/500 is small, and n = 1500 is high, we can apply Poisson. The mean of a binomial random variable is np, and we will substitute that as the parameter, lambda, representing the mean number of occurrences in a fixed period.

\\ P(X = s) = \frac{e^{-\lambda}\lambda^s}{s!} ; \lambda = np = (1/500)*1500 = 3\\ \\ P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2) \\\\ P(X = 0) = \frac{e^{-3}3^0}{0!} = 0.0497\\ \\ P(X = 1) = \frac{e^{-3}3^1}{1!} = 0.149 \\ \\ P(X = 2) = \frac{e^{-3}3^2}{2!} = 0.224\\ \\ P(X \leq 2) = 0.423

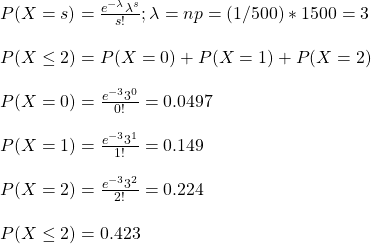
There is about a 42% chance that the error in five pages to remain not more than two.

Before we end, we should know the shortcuts to obtain the above results from the cumulative density functions (CDF). You may either look up the table or follow the R code.

#For Binomial 
pbinom(2, 1500, 1/500, lower.tail=TRUE)

# For Poisson
ppois(2, 3, lower.tail=TRUE)

Related Posts