Roulette stories are back. We will generate thousands of games with R programming utilising the probability of winning in a typical Roulette game. The sample function in R can produce random output at the specified probability values. For example,
sim_p <- (18/38)
sim_q <- 1 - sim_p
sample(c(1,-1), size = 1, prob = c(sim_p, sim_q), replace = TRUE)The above code will generate payoffs for even-money bets (odd/even, red/black) using the probabilities for success = (18/38) and failure = (20/38). If you win, you get $1; else, you lose $1. If you play more than one, provide that number at the size option.
Now, we will use the replicate function to generate hundreds of copies of the same calculation, simulating the scenario of several players gambling and will estimate various statistics. For simulating 1000 players,
B <- 1000
gamble <- replicate(B, {
gamble <- sum(sample(c(1,-1), size =1, prob = c(sim_p, sim_q), replace = TRUE))
})The code gives the total amount that each of the 1000 players gets. Now, put the whole calculations in a for-loop and estimate the money each player gets by playing up to 10000 games. Then evaluate two statistics: the average amount of total money a player could get and the number of players who made money (> $0) in the betting.
sim_p <- (18/38)
sim_q <- 1 - sim_p
game_x <- 10000
game_nu <- seq(1:game_x)
win_nu <- seq(1:game_x)
win_mon <- seq(1:game_x)
for (game in 1:game_x){
B <- 1000
win_amt<- replicate(B, {
amount <- sum(sample(c(1,-1), size = game, prob = c(sim_p, sim_q), replace = TRUE))
})
game_nu[game] <- game
win_mon[game] <- mean(win_amt)
win_nu[game] <- sum(win_amt > 0)
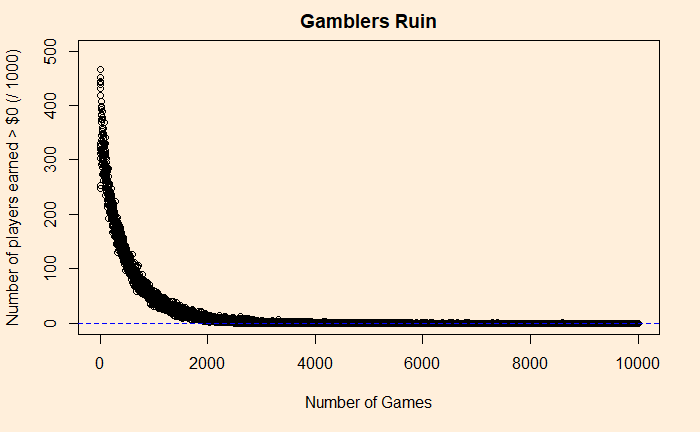
}The out gives three vectors – game_nu, win_mon, and win_nu for, respectively, game number, total money gained and the number of people (out of 1000) who won at least a dollar in the end. The plots are below.
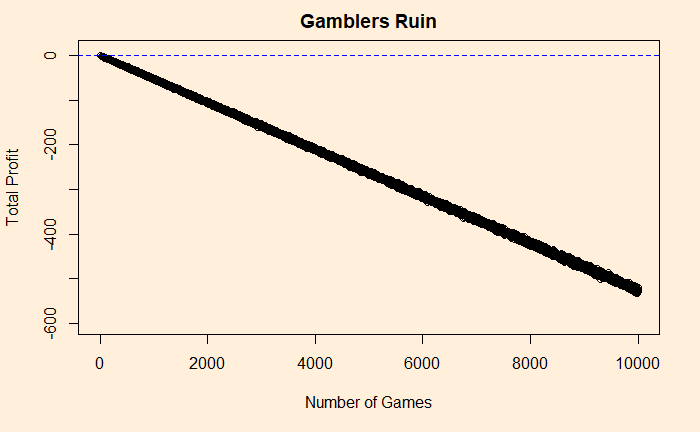
Note that the first graph represented the average loss, which averaged over 1000 players. And that is the reason why it appears as a neat, straight line. In reality, it will be a scatter like the following.
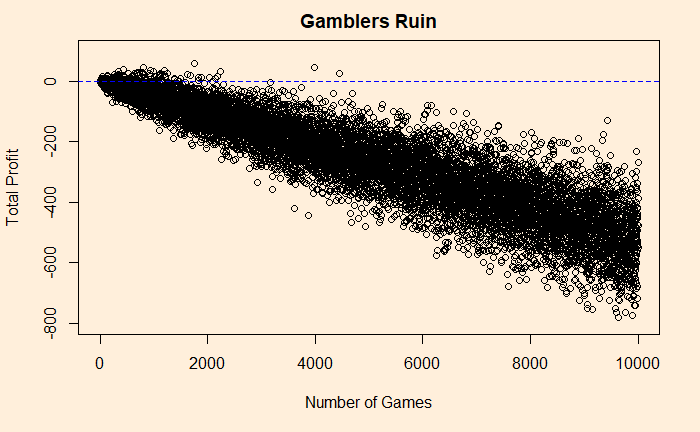
Yes, a few players can still make a dollar after playing 2000-3000 games (as seen in graph 2). Beyond that, not even a single player makes anything positive.

