Waiting for Heads

The last time, we saw the expected waiting times of sequences from coin-flipping games. Today, we will make the necessary formulation to theorise those observations.

We have already seen how the expected values are calculated. In statistics, the expected values are the average values estimated by summing values multiplied by the theoretical probability of occurrence. Start with the simplest one in the coin game.

Consider a coin with probability p for heads and q (= 1-p) for tails. Note that, for a fair coin, p becomes (1/2).

Expected waiting time for H

You toss a coin once: it can land on H with probability p and T with q or (1 -p). If it is H, the game ends after one flip. The value (for the time to wait) becomes 1, and the expected value, E(H), for an H start is p x 1. On the other hand, if the flip ends up with T, you start again for another flip. In other words, you did 1 flip, but back to E(H). The expected value, in this case, is (1-p)x(1 + E(H)). The final E(H) is the sum of each starting possibility.

\\ E(H) = p*E(H1) + q*E(T1)\\ \\ E(H) = p*1 + (1-p)*(1 + E(H)) \\ \\ p*E(H) = p + 1 - p \\ \\ E(H) = \frac{1}{p} = 2 \text{, for a fair coin (p = 1/2)}

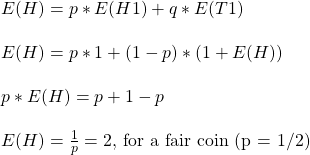
This should not come as a surprise. Since p is the probability of getting heads (say, 1/2), you get an H on an average 1/p (2) flip if you flip several times.

Expected waiting times for HT

We follow the same logic again. You made one flip (1), and you have two possibilities as starting – p x E(HT|H) and q x E(HT|T). HT|H means H followed by T given H has happened. For the second flip, you either start from the state of H or from the state of T.

\\ E(HT) = 1 + p*E(HT|H) + q*E(HT|T) \\ \\ \text{from the state of H, } \\ \\ E(HT|H) = p*(1 + E(HT|H)) + q*1 \\ \\ E(HT|H) = \frac{p + q}{1 -p} = \frac{1}{0.5} = 2\\ \\ \text{from the state of T, } \\ \\ E(HT|T) = p*(1 + E(HT|H)) + q*(1 + E(HT|T)) \\ \\ E(HT|T) = 0.5*(1 + 2) + 0.5*(1 + E(HT|T)) \\ \\ E(HT|T) = \frac{0.5*(1 + 2)}{0.5} + \frac{0.5}{0.5} = 4 \\ \\ E(HT) = 1 + p*2 + q*4 = 1+1+2 = 4

Expected waiting times for HH

We’ll use a different method here.

\\ \text{If the first toss is a T, } \\ \\ term1 = q*(1+E(HH)) \text{; start again with the same expected time, E(HH), after the first T}\\ \\ \text{First toss is an H and the two tosses are HT } \\ \\ term2 = p*q*(2+E(HH)) \text{; start again after the second, T}\\ \\ \text{First toss is an H and the two tosses are HH, and you win in 2 tosses} \\ \\ term3 = p*p*2 \\ \\ E(HH)) = term1 + term 2+ term3 = q*(1+E(HH)) + p*q*(2+E(HH)) + p*p*2 \\ \\ E(HH)) = 0.5 + 0.5*E(HH)) + 2*0.5*0.5 + 0.5*0.5*E(HH) + 0.5*0.5*2 \\ \\ E(HH)) = \frac{0.5+2*0.5*0.5+0.5*0.5}{0.25} = \frac{0.5+2*0.5*0.5+0.5*0.5*2}{0.25} = \frac{1.5}{0.25} = 6

Related Posts