What is an easy way to show that speed cameras reduce the number of accidents? Why are superstar children have a higher probability of not meeting their parent’s performance levels? Why do the popularities of movie-sequels dip compare to the originals?
There is a standard statistical phenomenon that connects the questions mentioned above. It is called regression to the mean. Regression is a process to establish a mathematical relationship between an observation and the variables that, we think, are responsible for the observation. In the mathematical language:
observation = deterministic model + residual error
By the way, the error does not mean a mistake but the sum of all random contributions (which was not explainable).
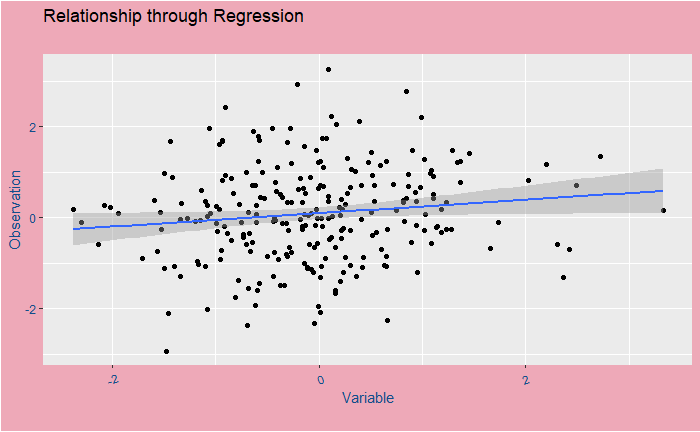
Regression to mean
The data points in the above plot represent a fictitious relationship between an observation and its variable. The blue line that passes through those points is the regression line or the best-fit line corresponding to a simple mathematical relation. In other words, following that line will tell you the expected value (mean) of the observation at any future value of the variable.
But the reality is the dots, all over the place but smoothly arranged around the line. Here is an important thing: if you see an observation above the line, the possibility for the next one to come below is high so that the average falls on the line. The opposite is true for an observation below the line.
Blockbusters and accidents
What is common to all those situations described in the beginning? One factor is that we selected extreme values, superstars, superhit moves. In other words, we tend to pick up only the points that are either lower or higher than the regression lines to draw comparisons. So, naturally, the next one (the children, luck, number of accidents, the height of people) has to come dramatically lower (if we talk about top events) or higher (if bottom events).
To end
The most suitable places to keep the speed cameras are the locations with the highest number of accidents because those are unlikely to retain their ranks even without cameras. Similarly, the likelihood of matching the pinnacle of success is small for the star personalities or the blockbuster movies considered for making a sequel.

