The last two posts ended with rather pessimistic notes on the possibility of establishing justice under the complex world of overlapping pieces of evidence. We end the series with the last technique and check if that offers a better hope of overcoming some inherent issues of separating signals from noise using the beta parameter.
Beta comes from signal detection theory, and it is the ratio of likelihoods, i.e. P(xi|G)/P(xi|I). P(xi|G) is the probability of the evidence, given the person is guilty, and P(xi|I), if she is innocent.
Let us start from Bayes’ rule,
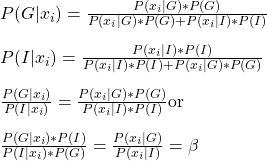
So, beta depends on the posterior odds of guilt and the prior odds of innocent.
For a situation at a likelihood ratio of 1, if the prior belief, P(G), is lower, the jury is less likely to make a false alarm. Graphically, this means moving the vertical line to the right and achieving higher accuracy in preventing false alarms (at the expense of more misses).
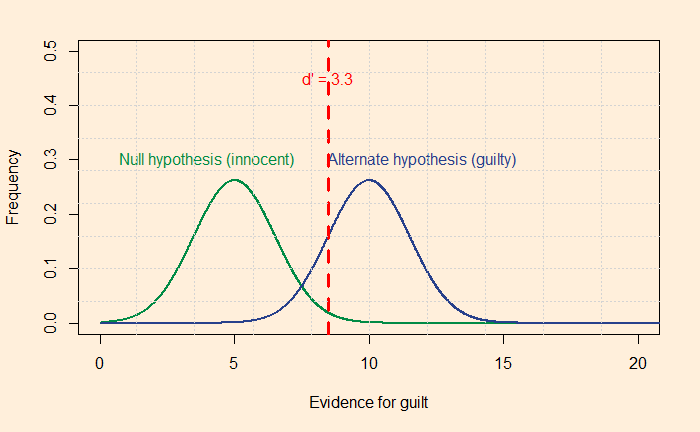
The sad truth is that none of these techniques is helping to reduce the overall errors in judgement.
Do juries meet our expectations?: Arkes and Mellers

