Shaquille’s story continues. Last time, we made assumptions about each other’s feelings (hypotheses is the polished word!) for Shaq’s chance to enter the White House. Those assumptions were arbitrary: 0.9 and 0.2 for the probability of success or p. What about other factions? There are infinite of them between 0 and 1. This time, we will make no assumptions and take as many as possible using a continuous hypothesis generator.
For that purpose, we will use the beta distribution function. Why beta? There is a reason for that, but we will know only towards the end. For now, we focus on what it can do for us more than what beta is. The beta distribution function can give a wide variety of probabilities for the entire range of p values. See three typical types (beta pdf uses two characteristic parameters, alpha and beta):
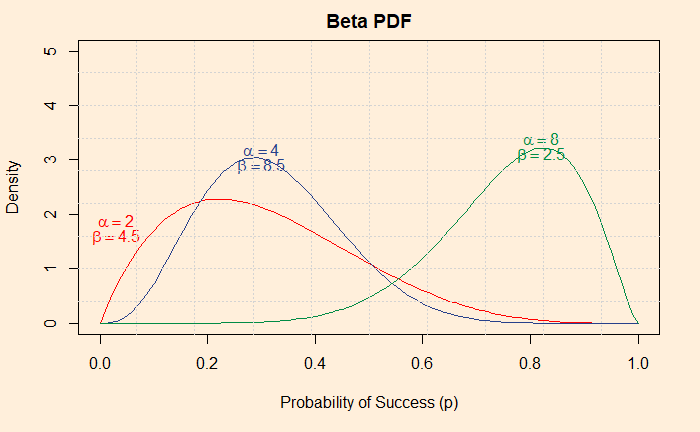
And three variety types:
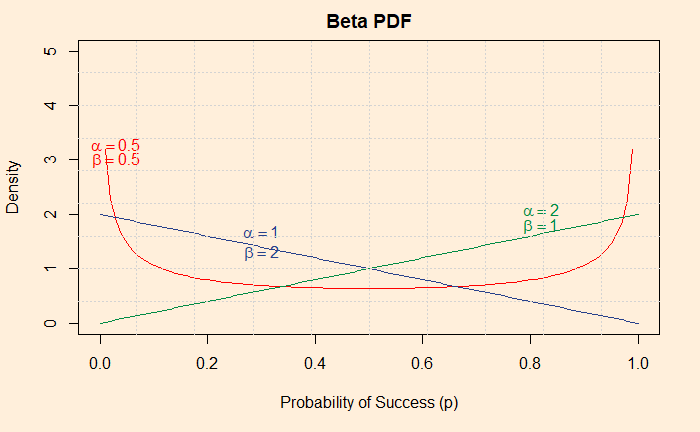
The first reason to choose the beta distribution function (don’t get confused; this is not a beta function, which is a different beast) is that it takes the range of hypotheses (p) we are after as its input. i.e. 0 to 1.
What should Shaq and his friend choose?
Remember, Shaq and his friend have strong views about getting inside the White House, and they are betting! So, which shape of the beta distribution function should they choose? They are unlikely to use more consensus-driven types, the curves that bulge in the middle. Who will bet when two opinions are towards a single idea? So, they chose alpha = 0.5 and beta = 0.5 as their prior hypothesis.
Bayes’s to help after the misadventure
We know what happened: Shaq failed to get inside without the prior appointment, so the outcome was zero success in the first attempt. Now, we predict what happens if he tries again (without actually doing and finding it). That is where Bayesian inference comes in handy. That is also the second reason for choosing the beta distribution function. Write down the Bayes’ rule here, i.e. posterior = likelihood x prior / sum of all possibilities. In the world of continuous functions, integrations replace additions.

Then a miracle happens: a complicated equation applied over the prior beta function results in a posterior beta function with a few minor modifications. The posterior is:
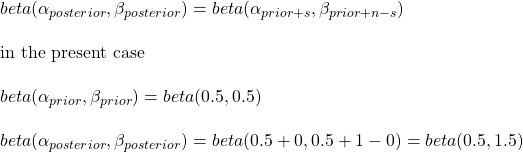
New betting scheme
You know why s was zero and n was one, because Shaq did one (n) attempt and failed (s)! How does the new scenario, beta(0.5, 1.5), look? Here is the shape of beta(0.5, 1.5):
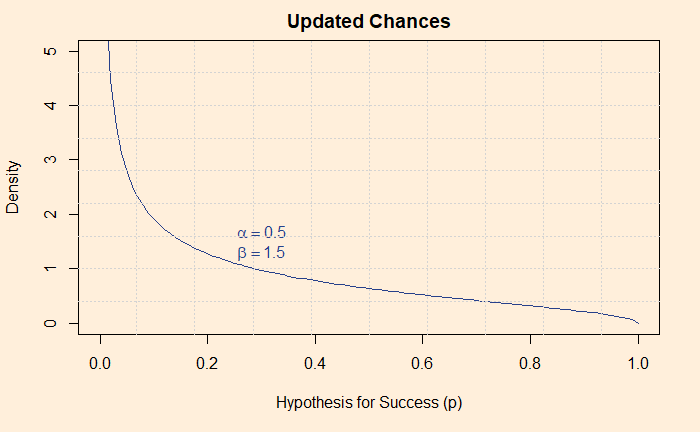
Putting together
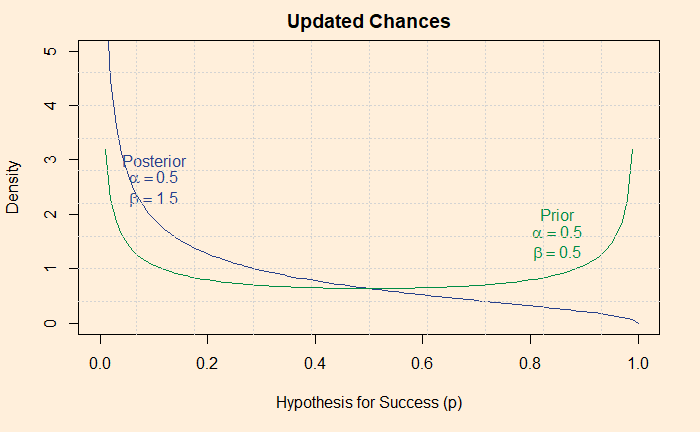
The updated chance of Shaq getting inside the White House has come down after the information that he failed in his first attempt came out.
Shaq Denied Entrance: Washington Post
Bayesian Statistics for Beginners: Donovan and Mickey

