Do you remember the shopping mall example? The one which attracts about 6000 customers a day? Now your task is to establish an expected value, the number of customers in a given day, and a confidence interval around it. You have the customer visits from the previous week as a reference.
| Day | Number of Visitors |
| Monday | 6023 |
| Tuesday | 6001 |
| Wednesday | 5971 |
| Thursday | 6045 |
| Friday | 5970 |
| Saturday | 5950 |
| Sunday | 6040 |
The simplest way is: find out the mean, assume a distribution, and calculate the standard error. Let’s do that first. Since the number of visitors is counts, and we think their arrivals are random and independent (are they?), we choose to use Poisson distribution. Average of all those numbers give 6000, so it is
![]()
In English, it meant: for fetching the distribution of counts at a given average (mu), we decided to use a Poisson distribution with a parameter mu.
The advantage of using the Poisson is that we can now get the variance easily. For Poisson, the mean and variance are both the same, equal to mu = 6000. Therefore,
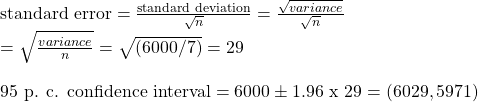
Bayesian Statistics
By now, you may have sensed that the best way to capture the uncertainties of customer visits is to consider the average too as a variable. After all, the present mean (6000) is just from a week’s data. Since the average is no more limited to integers but can also be fractions, we go for continuous distributions such as Gamma distribution to represent. In other words, a distribution of mu is my prior knowledge of average. And our objective is to get the updated mu or the posterior. So we are finally at the Baysian space for distributions or Bayesian statistics.
In Summary
You use the prior knowledge of the expected value (or average) through a Gamma distribution and apply it to the variable defined by a Poisson distribution. No marks for guessing: the posterior will be a Gamma! We will complete the exercise in the next post.

