Having seen people’s behaviour—whether wearing a raincoat or not—here is the question: Given that you have seen someone wearing a normal coat, what is the probability that it will be a sunny day? For reference, here is the hidden Markov tree.

In the usual math shorthand, we need to find P(S|NC). We can use the Bayes theorem here.
P(S|NC) = P(NC|S) x P(S) /[P(NC|S) x P(S) + P(NC|R) x P(R)]
P(NC|S) = probability of wearing a normal coat given it’s sunny. We know it is 0.9
P(NC|R) = probability of wearing a normal coat given it’s rainy. It is 0.4
P(S) = prior probability of today being sunny, i.e., without any clues from the dressing.
P(R) = 1 – P(S)
The probability of today being sunny
That can be estimated from the transition probabilities as follows. Here is the sunny part of the tree.
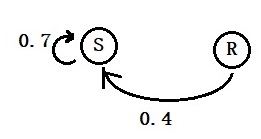
S = 0.7 S + 0.4 R
On the other hand,

R = 0.6 R + 0.3 S
To solve the equations, we need one more: S + R = 1. They lead to,
P(S) = 4/7 and P(R) = 3/7.
Back to Bayes
P(NC|S) = 0.9
P(NC|R) = 0.4
P(S) = 4/7
P(R) = 3/7
P(S|NC) = 0.9 x (4/7) /[0.9 x (4/7) + 0.4 x (3/7)]
= (3.6/7) / [(3.6/7) + (1.2/7)] = 3.6/4.8 = 0.75

