Waiting for Heads – Markov Chains

Some time ago, we analytically estimated the expected waiting times of sequences HT and HH from coin-flipping games. Today, we calculate them using Markov chains.

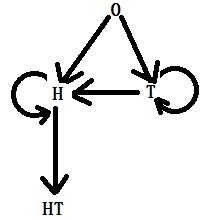
Waiting time for HT

First, the notations, followed by the transition matrix:

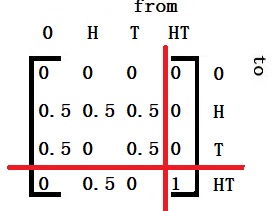
Get Q, I – Q and its inverse 

AA <- matrix(c(0.0, 0.5, 0.5,
               0.0, 0.5, 0.0,
               0.0, 0.5, 0.5), nrow = 3)

II <- matrix(c(1, 0, 0,
               0, 1, 0,
               0, 0, 1), nrow = 3)
BB <- II - AA

CC <- solve(BB)

NN <- c(1, 1, 1)
NN%*%CC

 4    2    4

The average waiting time from 0 to HT is the first element in the vector, i.e., 4.

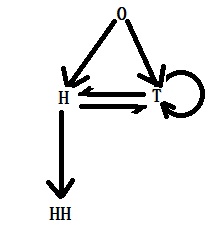
Waiting time for HH

AA <- matrix(c(0.0, 0.5, 0.5,
               0.0, 0.0, 0.5,
               0.0, 0.5, 0.5), nrow = 3)

II <- matrix(c(1, 0, 0,
               0, 1, 0,
               0, 0, 1), nrow = 3)
BB <- II - AA

CC <- solve(BB)

NN <- c(1, 1, 1)
NN%*%CC

 6    4    6

The waiting time is 6.