Absorbing chains – The Lawfirm

We have seen the concept of absorbing Markov chains. Here is a problem illustrating the idea.

A law firm has three types of employees: junior lawyers, senior lawyers, and partners. During a year
There is a 0.15 probability that a junior will get promoted to a senior
0.05 probability a junior leaves the firm
0.20 probability that a senior will get promoted to a partner
0.1 probability a senior leaves the firm
0.05 probability that a partner leaves the firm

What is the average number of years a junior stays in the company?

Step 1: Construct the transition probability matrix

J stands for junior, S for senior, P for partner, L for leaving and PL for partner leaving

\begin{bmatrix} 0.8 & 0.0 & 0.0 & 0.0 & 0.0\\ 0.15 & 0.7 & 0.0 & 0.0 & 0.0\\ 0.0 & 0.2 & 0.95 & 0.0 & 0.0\\ 0.05 & 0.1 & 0.0 & 1.0 & 0.0\\ 0.0 & 0.0 & 0.05 & 0.0 & 1.0 \end{bmatrix}

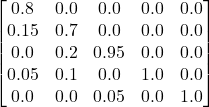
Step 2: Isolate I and make Q

If required, re-arrange the transition matrix and identify the unit matrix (corresponding to the absorbing).

After removing the columns and rows corresponding to the identity matrix, you are left with Q.

Q = \begin{bmatrix} 0.8 & 0.0 & 0.0\\ 0.15 & 0.7 & 0.0\\ 0.0 & 0.2 & 0.95 \end{bmatrix}

Step 3: Subtract Q from the Identity matrix

I - Q = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} - \begin{bmatrix} 0.8 & 0.0 & 0.0\\ 0.15 & 0.7 & 0.0\\ 0.0 & 0.2 & 0.95 \end{bmatrix}

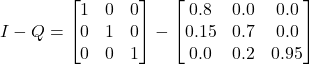
Step 4: Calculate the inverse of (I – Q)

The whole process so far is

Q <- matrix(c(0.8, 0.15, 0,
               0.0, 0.7, 0.2,
               0, 0.0, 0.95), nrow = 3)

I <- matrix(c(1, 0, 0, 
               0, 1, 0, 
               0, 0, 1), nrow = 3)
I_Q <- I - Q

I_I_Q <- solve(I_Q)
5.0   0.000000    0
2.5   3.333333    0
10.0 13.333333   20

Add numbers corresponding to each category (column) to determine the average number of stages (years). For example, a junior to stay 5 + 2.5 + 10 = 17.5 years. A senior will remain at an average of 3.3 + 13.3 = 16.6, and Partners will persist an average of 20 years before leaving.

Related Posts