Amy lives in city A and has friends in cities B, C, D, and E. The following scheme represents the direct bus connections to these cities. Every Monday, she takes a direct bus at random, reaches the town, and stays with her friend for a week. How many weeks would she have spent in each city that year if she had done this for a year?
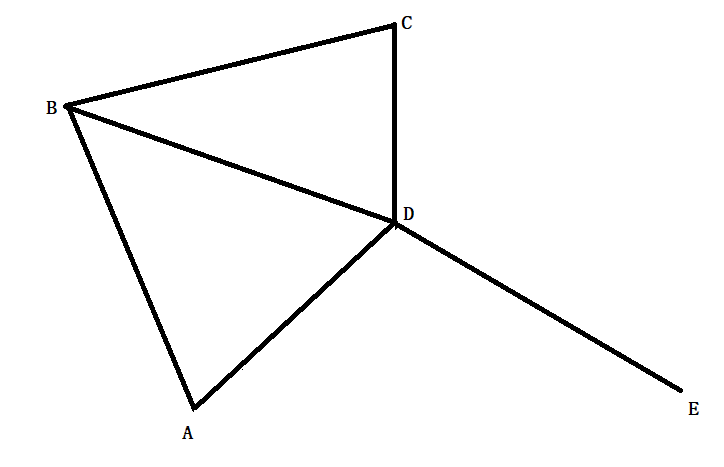
The route map suggests that on a given week, Amy has the following probabilities
1) Equal chances from A to B or D (0.5, 0.5)
2) Equal chances from B to A, C, or D (0.33, 0.33, 33)
3) Equal chances from C to B, D (0.5, 0.5)
4) Equal chances from D to A, B, C or E (0.25, 0.25, 0.25, 0.25)
5) Can move from E to D (1.0)

In the matrix form
0.0 0.33 0.0 0.25 0.0
0.5 0.00 0.5 0.25 0.0
0.0 0.33 0.0 0.25 0.0
0.5 0.33 0.5 0.00 1.0
0.0 0.0 0.0 0.25 0.0The required task is to find the stable end distribution of cities, which can be done using the relationship.
P X* = X*

The expansion of the above equation leads to the following linear relationship that we will solve analytically.
0A + 0.33B + 0C + 0.25D + 0E = A
0.5A + 0B + 0.5C + 0.25D + 0E = B
0A + 0.33B + 0C + 0.25D + 0E = C
0.5A + 0.33B + 0.5C + 0D + 1E = D
0A + 0B + 0C + 0.25D + 0E = E
A + B + C + D + E = 1
Substitute for A in the first equation and solve the set of 5 linear equations using the following R program.
A <- matrix(c( 0.0, 0.5, 0.0, 0.50, 0.0,
1.333, -1.0, 0.333, 0.333, 0.0,
1.0, 0.5, -1.0, 0.5, 0.0,
1.25, 0.25, 0.25, -1.0, 0.25,
1.0, 0.0, 0.0, 1.0, -1.0), nrow = 5)
B <- c(1, 0, 0, 0, 0)
solve(A, B)0.16686465 0.25007815 0.16661457 0.33335417 0.08333854
