We have seen one type of ultimatum game where the player who receives the offer (Annie) has another option outside the one in the game. Those options are a weak type (0.25) or a strong type (0.5) and depend on a probability p in favour of the former.
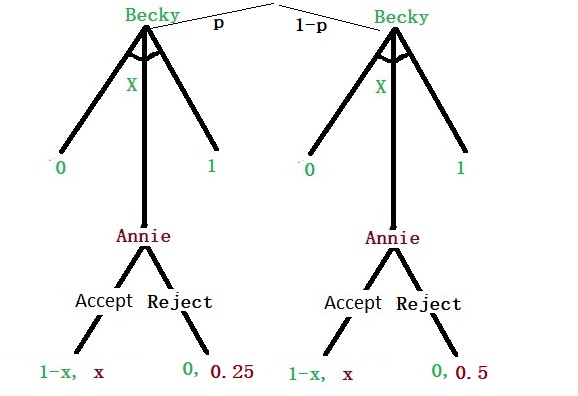
Now, imagine Becky knows Annie’s outside option (0.25 vs 0.5). In that case, Becky will make 0.25 p times and 0.5 (1-p) times to get her offer accepted.
If p < 2/3
Becky will offer 0.25 (2/3)rd of the time and 0.5 (1/3)rd of the time. Her expected value of surplus in the case of complete information is
p x (0.75) + (1-p) x (0.5)
Note that in the case of incomplete information, she would have offered 0.5 all the time, leading to the expected value
p x (0.5) + (1-p) x 0
The difference between the two [p x (0.75) + (1-p) x (0.5) – p x (0.5)] is 0.25p. It is the value of information.
If p > 2/3
In the case of complete information, Becky will offer 0.5 (2/3)rd of the time and 0.25 (1/3)rd of the time. Her expected value of surplus is
p x (0.75) + (1-p) x (0.5)
Note that in the case of incomplete information, she would have offered 0.25 all the time, leading to the expected value
p x (0.75) + (1-p) x 0
The difference between the two [p x (0.75) + (1-p) x (0.5) – p x (0.75)] is 0.5(1-p). It is the value of information.
Bargaining 101 (#24): William Spaniel

