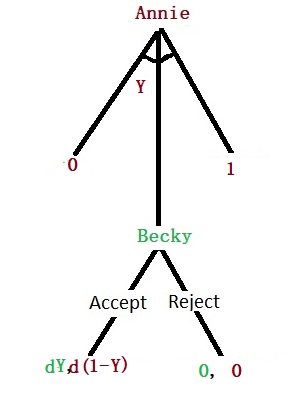
We have seen the first level of bargaining – the ultimatum game. Becky made the offer for Annie’s car, and the latter will accept or reject it. The decision tree that we have seen before can be drawn as a fraction of the surplus:

In the next level, Annie can make a counteroffer instead of rejecting the offer. Here is the game:

The above picture suggests that Annie offers Becky a fraction of the surplus in her counteroffer. But there is a small problem. Since the counteroffer and the decision consume more time than the take-it-or-leave-it situation, the benefit from the subsequent game must be discounted (time value of money) by a fraction d.

Let’s solve the problem, as before, from the end backwards.
The solution is exactly like before, and the answer is that Annie will get the entire surplus, and Becky has no bargaining power. Here is the whole picture.
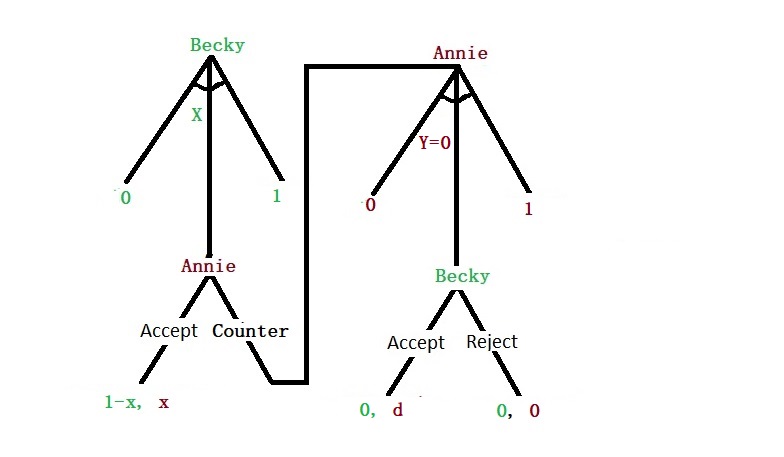
And to the start of the tree.
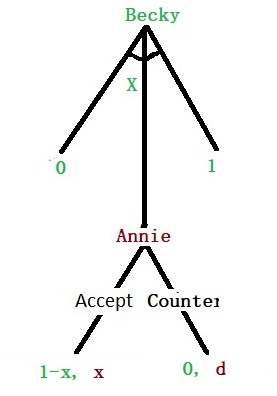
Now, Becky must decide what X should be, as she knows Annie can reject the offer and get a payoff of d. In that case, Becky will get zero. The solution that Annie accepts, therefore, is X = d. Annie is getting d, and Becky will get (1 – d) of the surplus.

