In the last post, we have seen how banks make money by lending. To get estimates of profits and probabilities, we have assumed two conditions – independence and randomness. This time we look at cases where both these assumptions don’t hold.
Our bank is now making about 1.8 million annual returns with 2000 customers, who have been handpicked for their high credit scores and predictability to repay.
Want for More
An idea was proposed to the management to expand the firm and to increase the customer base. The argument was that even though adding more customers can reduce the predictability of defaulting, the risks could be managed by raising the interest rate a bit higher. Assurance was given that even for an assumed default rate of 5%, which is double the existing, by increasing the interest rate to 6.3%, the bank can make up about 8 million with 99% confidence. She has rationalised her calculations based on the law of large numbers, that the bank is unlikely to miss the target.
The expected value of profit = [interest rate x profit per loan x (1-default rate) – cost per foreclosure x default rate] x total number of loans.
For 20,000 loans, this will mean
[0.063 x 9000 x (1-0.05) – 100,000 x (0.05)] x 20,000
an earning of about 8 millions!
She further shows a plot of the simulation to support her arguments.
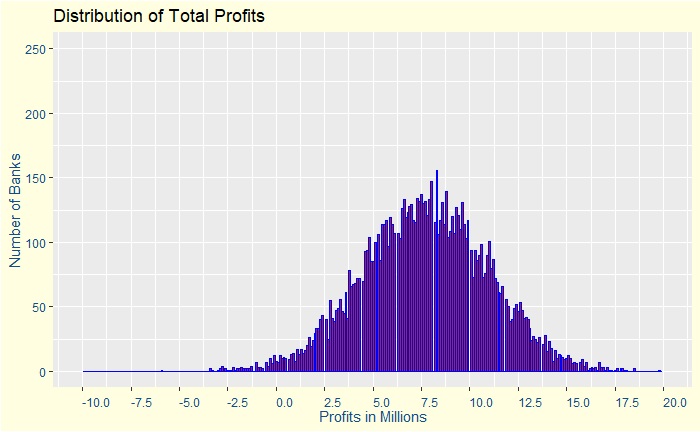
It convinced the management, and the company is now on an aggressive lending campaign. The firm has now 20,000 customers and makes a lot of money. A few months later comes a global financial crisis, and the firm is now bankrupt.
Assumption of Independence
To understand what happened to the bank, we should challenge the assumptions used in the original statistical calculations, especially the independence of variables – that one person defaults does not depend on the other. When there are many borrowers with varying capacities to repay, such crises prove detrimental to the business.
Assume a 50:50 chance, up or down, for everyone to default by a tiny fraction + / – 0.01 (1%) or between 0.04 and 0.06. Note that the average risk of default is still 5% but are no longer independent. Subsequently, the overall chances for making a loss has moved from 1% to 31%, but the average return is still around 8 million. A plot of the distribution of profits is below.
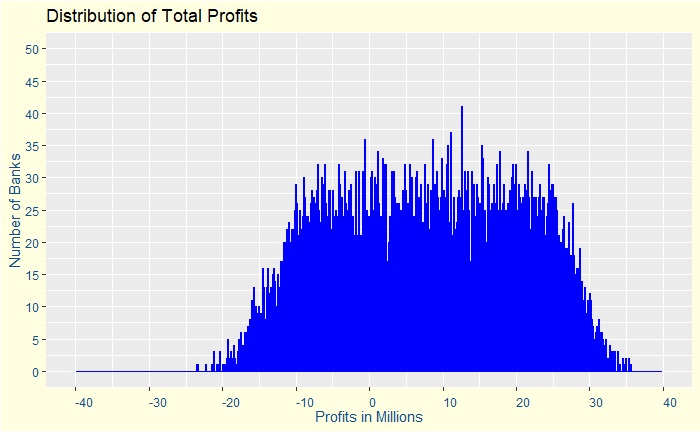
The plot is far from a uniform distribution as the central limit theorem would have predicted using an assumption of complete independence of variables.

