There are two players in the duel game, P1 and P2. Each carries a pistol loaded with a single bullet positioned a certain distance apart. Each player gets one round at a time, one after another. A player can shoot the other or step forward in her turn. Whoever hits the other wins the game. So, the player’s strategic decision is when she should shoot.
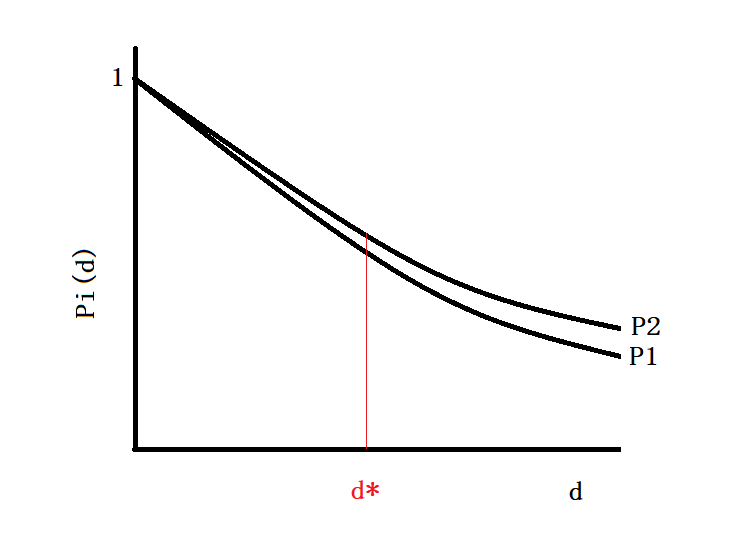
Let Pi(d) be the probability that player i will get her target (the opponent) from a distance d. The two players can have different abilities. In other words, P1(d) can be lower (or higher) than P2(d). Also, at d = 0, P1 and P2 hit the target (P1(0) = P2(0) = 1).
So, who will take the shot first, and when?
Imagine it’s P1’s turn, and she can believe in the following two things:
1) P2 will not shoot in the next turn
2) P2 will shoot in the next turn
If P1 believes in option 1 (that P2 will not shoot in the next turn), P1 will not shoot in this turn. If P1 thinks that P2 will shoot, then P1 will evaluate her options in the following manner. If P1 thinks her probability of hitting the target in this turn is greater than or equal to her opponent’s chance to miss in the next turn, she will shoot. Mathematically, that is:
P1(d) >/= 1 – P2(d-1) or
P1(d) + P2(d-1) >/= 1
The distance at which the condition is satisfied is d*. From the picture, it is clear that below d*, the probability, P1(d) + P2(d-1) > 1 and above d*, it is < 1.

