The sign test is a simple non-parametric test. In the last example, we went for the median of a group, classified people as + or – based on the null hypothesis and evaluated the p-value.
Here are 10 individuals undergoing a particular diet. Their haemoglobin levels are measured. Note that levels below 13.0 g/dL qualify a person as anaemic. What is your conclusion regarding the possibility of this diet inducing anaemia?
| Case # | Drug A |
| 1 | 12.3 |
| 2 | 13.1 |
| 3 | 11.3 |
| 4 | 10.1 |
| 5 | 14.0 |
| 6 | 13.3 |
| 7 | 10.5 |
| 8 | 12.3 |
| 9 | 10.9 |
| 10 | 11.9 |
Our task is to assess whether the group’s median haemoglobin level is 13.0 or below. Needlessly, at a specified significance level, say at 5%.
The Null Hypothesis, H0: Median = 13.0
The Alternate Hypothesis, H1: Median < 13.0
Let’s re-draw the table after including the +/- convention – plus for > 13.0 and minus for < 13.0.
| Case # | Drug A | Sign |
| 1 | 12.3 | – |
| 2 | 13.1 | + |
| 3 | 11.3 | – |
| 4 | 10.1 | – |
| 5 | 14.0 | + |
| 6 | 13.3 | + |
| 7 | 10.5 | – |
| 8 | 12.3 | – |
| 9 | 10.9 | – |
| 10 | 11.9 | – |
A person unexposed to statistics and random variations may conclude that at least five observations are required above 13.0 for the null hypothesis to be valid. And since there are only three, the null hypothesis is rejected. But we know about randomness and distributions, and therefore, ask this question: What is the probability of having seven negative observations from a binomial trial that is expected to have a 50% chance of success?
P(>=7) = P(7) + P(8) + P(9) + P(10) = 0.117 + 0.044 + 0.0098 + 0.001 = 0.172. In the following figure, it is the sum of the heights of the red bars.
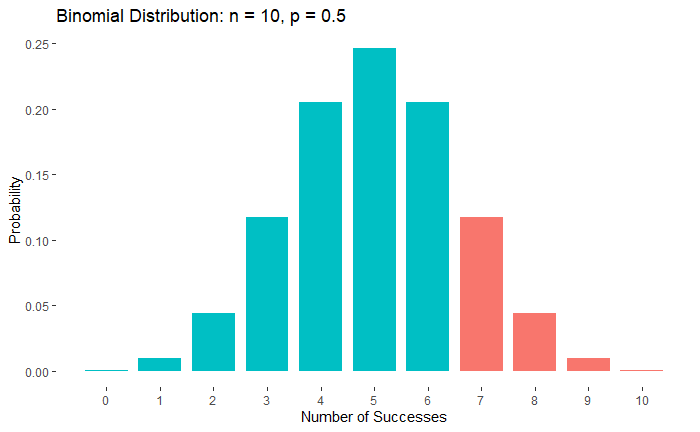
So, the observations are unable to reject the null hypothesis. Before we end, answer this question: How many observations must be below 13.0 for the null hypothesis to be true?
From the numbers and figure, it appears that you may need nine or ten observations below 13.0 for the sign test to make a rejection.
Does the magnitude of departure (from the median) play any role in rejecting the null hypothesis? We may have to explore another non-parametric test method, Wilcoxon signed rank, for that.
Non-parametric tests: zedstatistics

