Confusion Matrix and Statistics
Reference
Prediction Female Male
Female 55 24
Male 64 383
Accuracy : 0.8327
95% CI : (0.798, 0.8636)
No Information Rate : 0.7738
P-Value [Acc > NIR] : 0.0005217
Kappa : 0.4576
Mcnemar's Test P-Value : 3.219e-05
Sensitivity : 0.4622
Specificity : 0.9410
Pos Pred Value : 0.6962
Neg Pred Value : 0.8568
Prevalence : 0.2262
Detection Rate : 0.1046
Detection Prevalence : 0.1502
Balanced Accuracy : 0.7016
'Positive' Class : Female
We see the prediction we did had high overall accuracy. At the same time, we see it had a low sensitivity. It happened because of the low prevalence (proportion of females), 23%. That means failing to call actual females as females (low sensitivity) does not lower the accuracy as much as it would have by incorrectly calling males as females.
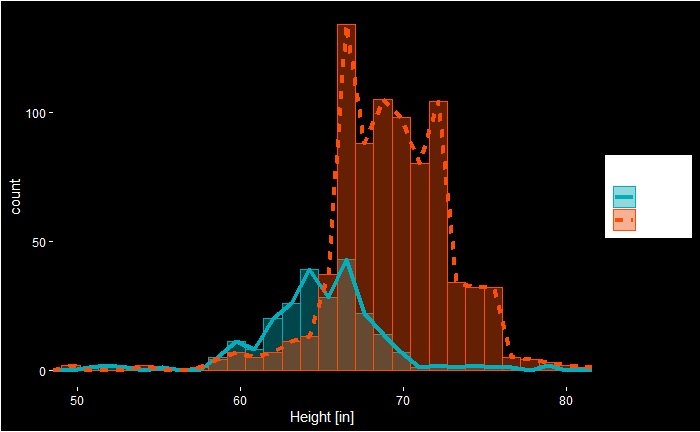
Here is the R code behind this fancy plot!
heights %>%
ggplot(aes(x = height)) +
geom_histogram(aes(color = sex, fill = sex), alpha = 0.4, position = "identity") +
geom_freqpoly( aes(color = sex, linetype = sex), bins = 30, size = 1.5) +
scale_fill_manual(values = c("#00AFBB", "#FC4E07")) +
scale_color_manual(values = c("#00AFBB", "#FC4E07")) +
coord_cartesian(xlim = c(50, 80)) +
scale_x_continuous(breaks = seq(50, 80, 10), name = "Height [in]") +
theme(text = element_text(color = "white"),
panel.background = element_rect(fill = "black"),
plot.background = element_rect(fill = "black"),
panel.grid = element_blank(),
axis.text = element_text(color = "white"),
axis.ticks = element_line(color = "white")) Looking at the plot, we see that the cut-off we used, 64 inches, misses a significant proportion of females. Let’s re-run the simulations after adding two more points (66 inches) to the cut-off.
Confusion Matrix and Statistics
Reference
Prediction Female Male
Female 82 66
Male 33 345
Accuracy : 0.8118
95% CI : (0.7757, 0.8443)
No Information Rate : 0.7814
P-Value [Acc > NIR] : 0.049151
Kappa : 0.5007
Mcnemar's Test P-Value : 0.001299
Sensitivity : 0.7130
Specificity : 0.8394
Pos Pred Value : 0.5541
Neg Pred Value : 0.9127
Prevalence : 0.2186
Detection Rate : 0.1559
Detection Prevalence : 0.2814
Balanced Accuracy : 0.7762
'Positive' Class : Female 
