In the previous post, we estimated the likelihood of getting six people sick for two parameters (prevalence), 7% and 8%. We can also calculate the ratio between the two likelihoods:
L(theta = 0.07 | data = 6) / L(theta = 0.08 | data = 6) = 0.153 / 0.123 = 1.24.
It means that the prevalence of 7% supports the data 1.24 times more than the prevalence of 8%. What about a sweep of likelihood over the entire parameter space? The function that gives the distribution of likelihoods of all possible values of parameters for a given data is the likelihood function.
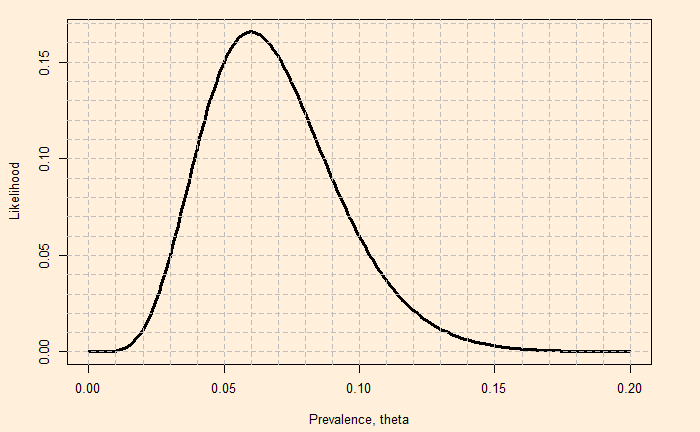
As the parameter (theta) defines a model (e.g., binomial probability mass function), what the likelihood function is telling us is, given I have this data, what is the chance that the given model is true? In other words, we want the model that is mostly to have produced our data.

