We have seen the likelihood ratio as the property of a diagnostic tool. Let’s take the fictitious screening tool we evaluated in the last post with LR+ = 10.7. Imagine a patient comes to a clinic with a few symptoms of a disease with a prevalence of 0.1 (very likely, age-adjusted), and this screening is a possible option. Would you recommend this? Note that the doctor will decide on further (costly) treatment only if she gets a conformation (posterior probability) of > 50% chance of the disease.
From the relationship we derived last time,
OR_Post = LR x OR_Pri
Odds ratio (posterior) = 10.7 x 0.11 = 1.07
P(poterior) / (1 – P(poterior)) = 1.88
1/P(poterior) = 1 + 1/1.88
P(poterior) = 1.88/2.88 = 0.54
A nomogram of the following type is built to make such calculations simpler.

Draw a line from the ‘pre-test probability’ to ‘the likelihood ratio’ and extend it to the ‘post-test probability line. The intersection gives the posterior probability.
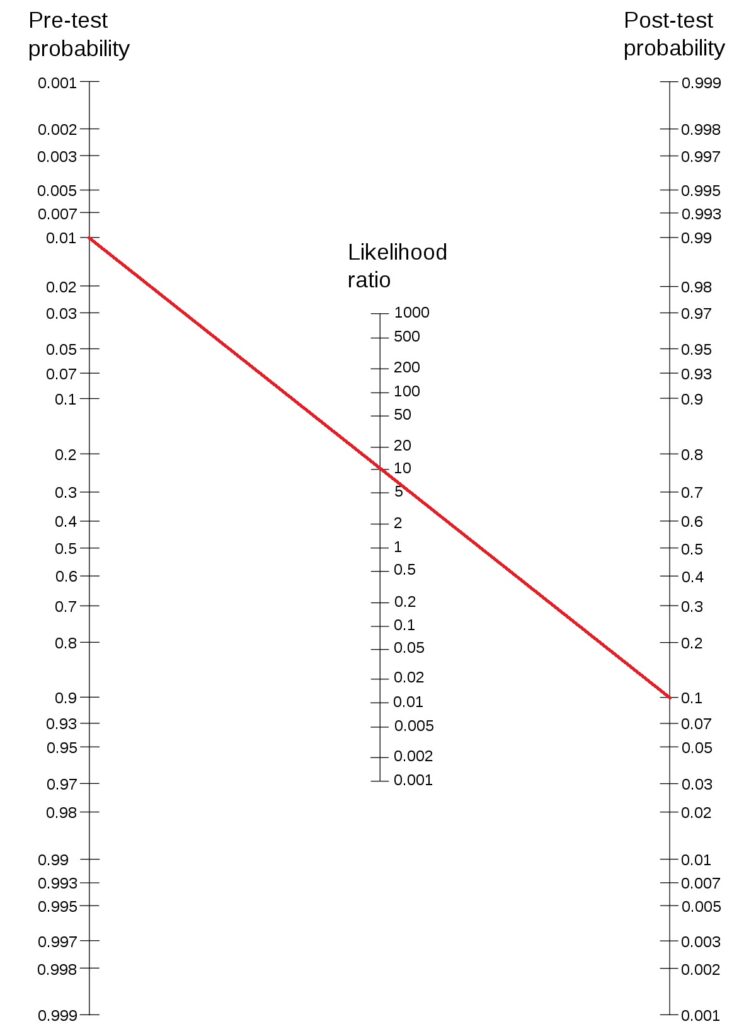
Here is an illustration of the method. Let’s use Fagan’s nomogram for the previous case,
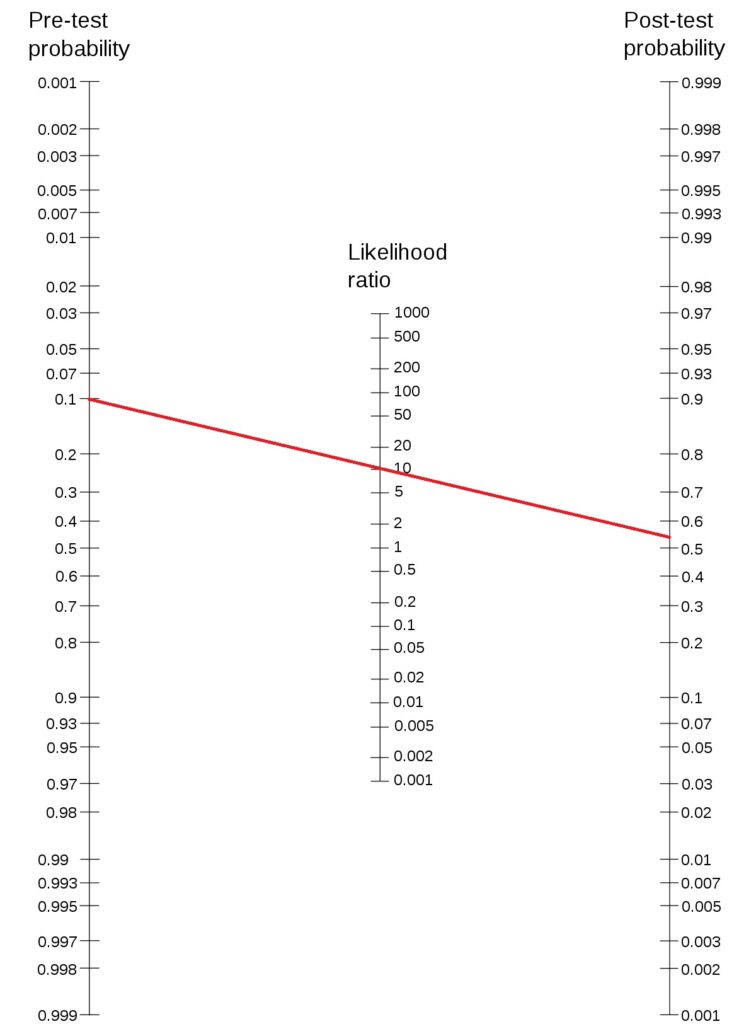
To answer the original question: this test may be recommended as it can bring the probability over 0.5 if the test comes positive. Not to forget, if the test comes negative (LR- = 0.044), the posterior probability becomes 0.005.
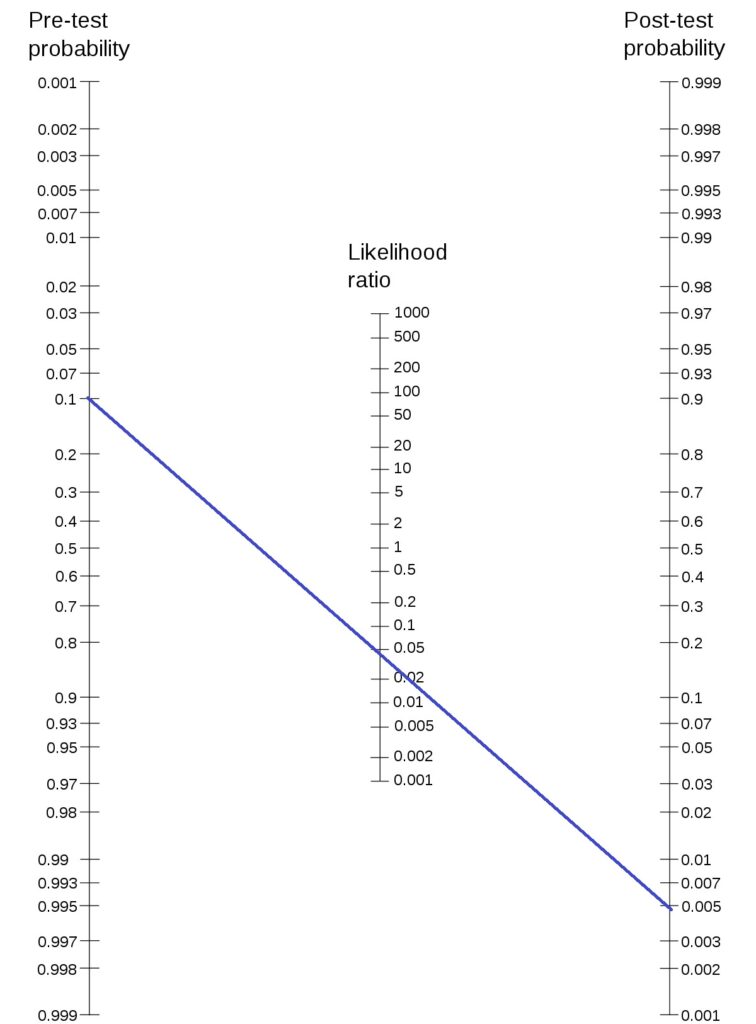
Smaller prior
On the other hand, if the prior probability is lower, say, 0.01, as you can see below, the test is not very useful to make a conclusive decision.
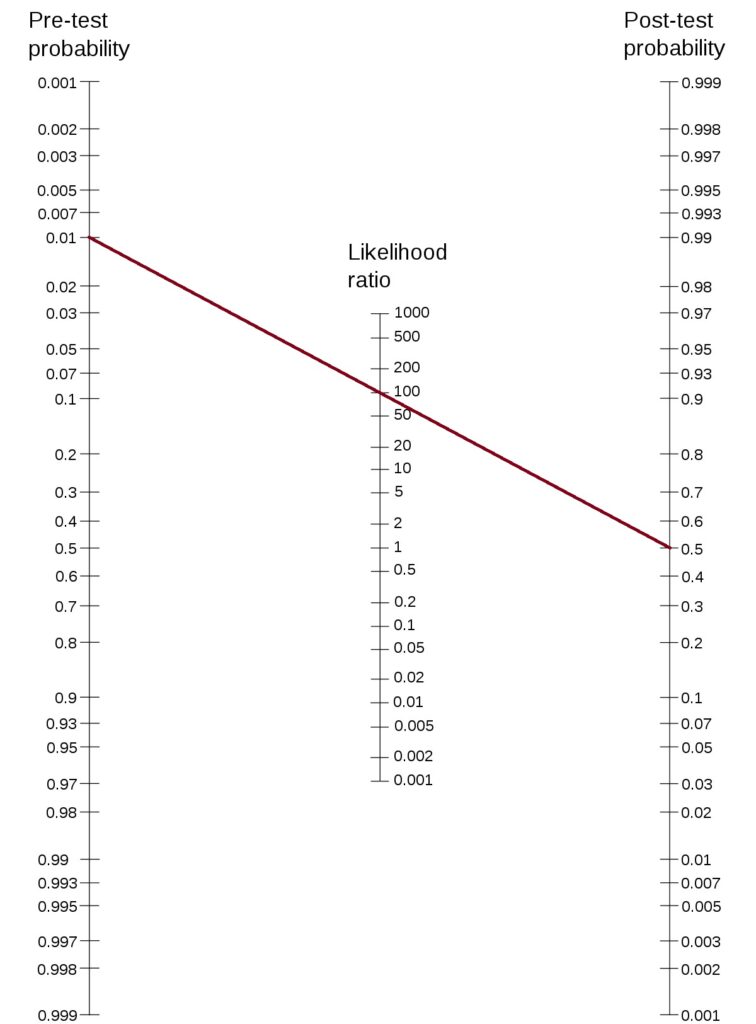
Such a disease would require a diagnostic tool with a likelihood ratio of 100 or above to make a decision. Connect 0.01 (prior probability) to 0.5 (minimum decision criterion) and find out the likelihood ratio.