We have seen how dice values are expressed as polynomials and how the resulting exponents become the sum and coefficients become the number of ways of obtaining the sum. Let’s extend this further and use dice rolling as a technique to estimate the production of polynomials.
(x + x + x^3 + x^4 + x^6 + x^6) * (x + x^2 + x^3 + x^3 + x^5 + x^6)
This is equivalent to two six-sided dice with the following numbers
dice 1: [1, 1, 3, 4, 6, 6]
dice 2: [1, 2, 3, 3, 5, 6]
Throw them a million times, estimate the probability and convert them into whole numbers.
dice_1 <- c(1, 1, 3, 4, 6, 6)
dice_2 <- c(1, 2, 3, 3, 5, 6)
prob_1 <- rep(1/6,6)
prob_2 <- rep(1/6,6)
itr <- 1000000
toss <- replicate(itr, {
sam1 <- sample(dice_1, 1, prob = prob_1, replace = TRUE)
sam2 <- sample(dice_2, 1, prob = prob_2, replace = TRUE)
sam <- sam1 + sam2
})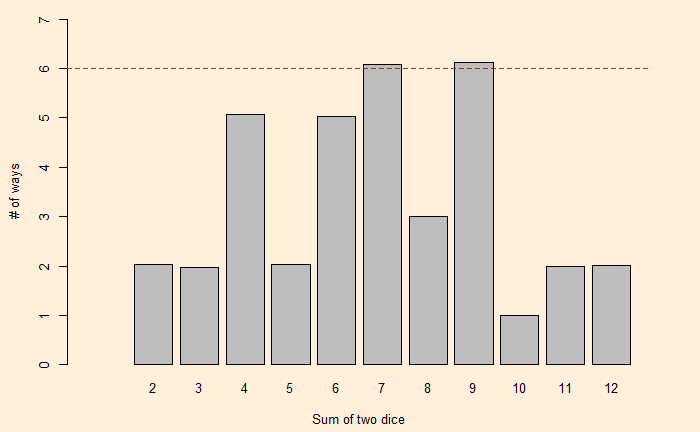
Let’s write down what we see above:
2x2 + 2x3 + 5x4 + 2x5 + 5x6+ 6x7 + 3x8 + 6x9 + x10 + 2x11 + 2x12
Estimate the product manually (or run it through the ‘Wolfram’ calculator )
2 x^2 + 2 x^3 + 5 x^4 + 2 x^5 + 5 x^6 + 6 x^7 + 3 x^8 + 6 x^9 + x^10 + 2 x^11 + 2 x^12
(x + x + x^3 + x^4 )*(x + x^2 + x^3 + x^3 + x^5 + x^6)
dice_1 <- c(1, 1, 3, 4)
dice_2 <- c(1, 2, 3, 3, 5, 6)
prob_1 <- rep(1/4,4)
prob_2 <- rep(1/6,6)
itr <- 1000000
toss <- replicate(itr, {
sam1 <- sample(dice_1, 1, prob = prob_1, replace = TRUE)
sam2 <- sample(dice_2, 1, prob = prob_2, replace = TRUE)
sam <- sam1 + sam2
})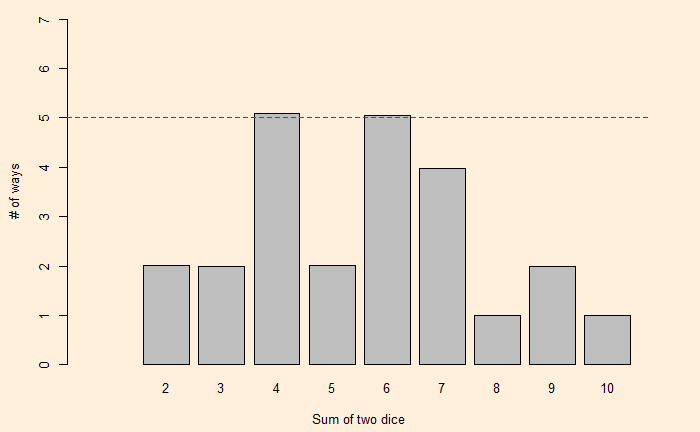
2x2 + 2x3 + 5x4 + 2x5 + 5x6 + 4x7 + x8 + 2x9 + x10
And the manual calculation gives:
2 x^2 + 2 x^3 + 5 x^4 + 2 x^5 + 5 x^6 + 4 x^7 + x^8 + 2 x^9 + x^10
(x + x + x3 + x4 )*(x + x2 + x3 + x3)
dice_1 <- c(1, 1, 3, 4)
dice_2 <- c(1, 2, 3, 3)
prob_1 <- rep(1/4,4)
prob_2 <- rep(1/4,4)
itr <- 1000000
toss <- replicate(itr, {
sam1 <- sample(dice_1, 1, prob = prob_1, replace = TRUE)
sam2 <- sample(dice_2, 1, prob = prob_2, replace = TRUE)
sam <- sam1 + sam2
})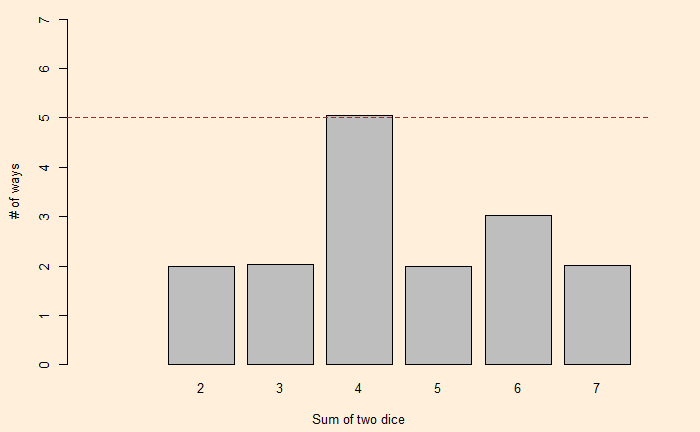
2 x2 + 2 x3 + 5 x4 + 2 x5 + 3 x6 + 2 x7
Online Factoring Calculator: Wolfram

