Logistic Regression and Challenger

Remember the post on the O-ring failure of the Challenger disaster?

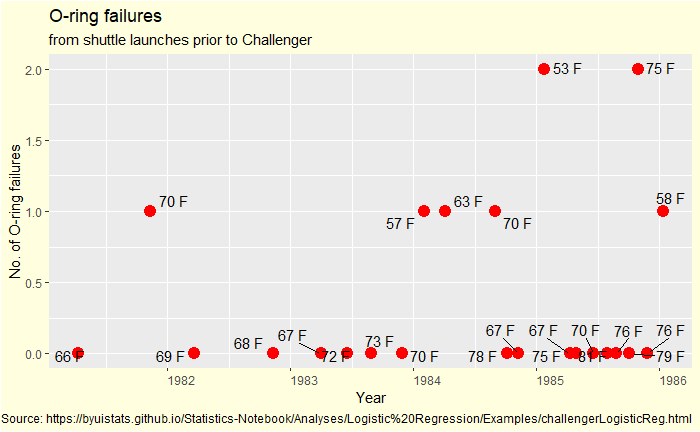
Here, we do a step-by-step logistic regression of the data. The following table shows the O-ring damages and launch temperatures of 24 previous shuttle launches. Damage = 1 represents failure, and 0 denotes no failure.

Flight #	Launch T (F)	O-ring Damage
STS 1	66	0
STS 2	70	1
STS 3	69	0
STS 4	80	0
STS 5	68	0
STS 6	67	0
STS 7	72	0
STS 8	73	0
STS 9	70	0
STS 41B	57	1
STS 41C	63	1
STS 41D	70	1
STS 41G	78	0
STS 51A	67	0
STS 51C	53	1
STS 51D	67	0
STS 51B	75	0
STS 51G	70	0
STS 51F	81	0
STS 51I	76	0
STS 51J	79	0
STS 61A	75	1
STS 61B	76	0
STS 61C	58	1

The logit function is:

$ln(\frac{P(Y = 1)}{1 - P(Y = 1)}) = Z = \beta_0 + \beta_1 X_i$

The beta values (the intercept and slope) are obtained by the ‘generalised linear model’, glm function in R.

logic <- glm(Damange ~ ., data = challenge, family = "binomial")
summary(logic)

Call:
glm(formula = Damange ~ ., family = "binomial", data = challenge)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.0608  -0.7372  -0.3712   0.3948   2.2321  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)  
(Intercept)  15.2968     7.3286   2.087   0.0369 *
Temp         -0.2360     0.1074  -2.198   0.0279 *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 28.975  on 23  degrees of freedom
Residual deviance: 20.371  on 22  degrees of freedom
AIC: 24.371

Number of Fisher Scoring iterations: 5

The following plot is obtained by substituting the values 15.2968142 and -0.2360207 in the function.

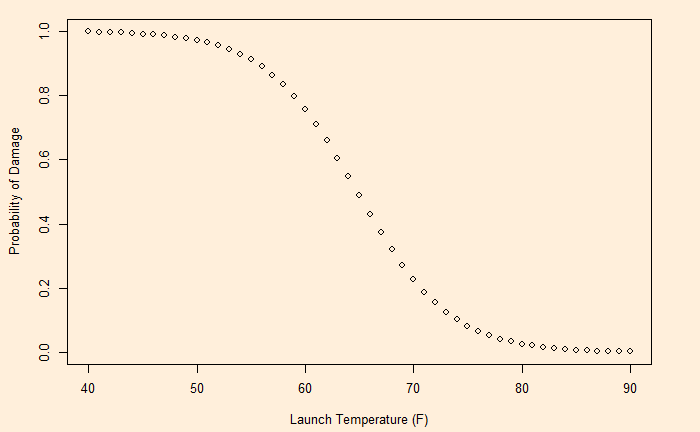
Having developed the probabilities, now it’s time for decision-making. That is next.

Related Posts