Negative Binomial Distribution

A fair coin is tossed repeatedly. What is the chance of getting 3rd head on the 10th toss?

You may notice the difference here; it is not asking for the probability of getting three heads in 10 tosses, which can be done using a binomial distribution. This one belongs to the negative binomial distribution.

Let each trial has a probability of success p (and failure 1−p). We follow this sequence until r successes occur.

The probability of observing the s success after having f failures (i.e., the success specified for the [s+f]th trial) is s+f-1Cf x ps x qf

The present problem

\frac{9!}{2! 7!} * (0.5)^3 * (1-0.5)^7 = 0.035

or the R – code

toss_number <- 10
success <- 3
failure <- toss_number - success
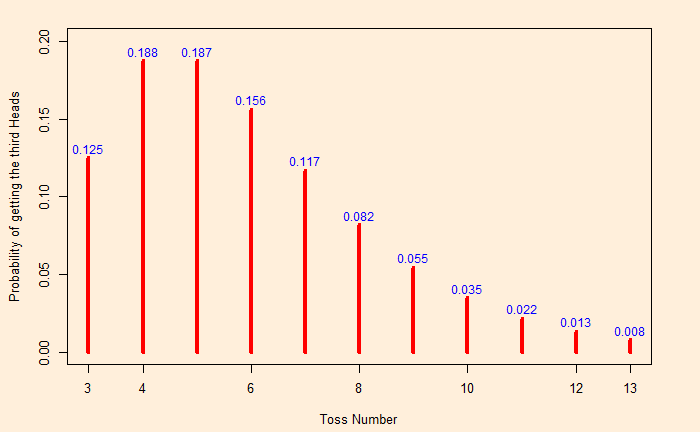
dnbinom(failure, success, prob = 0.5)
0.035

Here is the distribution of probabilities of success at each milestone.

Binomial and negative binomial

The key difference between the two is: in the binomial distribution, the number of trials is fixed and the number of successes is a random variable. Whereas in the negative binomial distribution, the opposite is true, viz. the number of successes is fixed and the number of trials is a random variable.

Related Posts