The Monty Hall problem has confused the heck out of people. It is a probability puzzle loosely based on an American game show, Let’s Make a Deal, once hosted by Monty Hall. The problem statement is as follows:
You are in a game show, and the host shows three closed doors behind which there are three objects – one car and two goats. Your task is to guess the correct door and win the car. Once you make the pick, the host opens one of the other two doors and shows you a goat. She now hands in a chance to switch your original choice. Will you stick with your original door or switch to the remaining unopened door?
The correct answer is: you better switch the door, but let’s work out how I arrived at this.
Method 1: Bayes’ Theorem
The equation of life! The equation is pasted below:
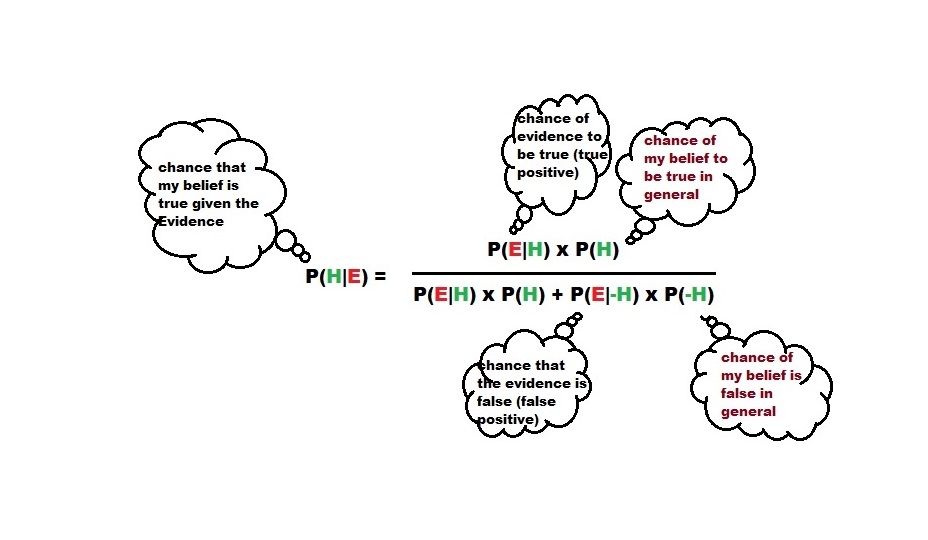
Turn that to fit our problem, the chance that my door is correct, provided the host showed me the goat, P(MyDoor|ShowGoat) =
P(ShowGoat|MyDoor) x P(MyDoor) / [ P(ShowGoat|MyDoor) x P(MyDoor) + P(ShowGoat|OtherDoor) x P(OtherDoor)]
P(ShowGoat|MyDoor) = chance of the host showing a goat in that door if my choice is right = 0.5 (or 50% chance to pick one of the remaining doors as both have goats)
P(MyDoor) = prior chance of my door having a car = 0.33 (or 1 in 3, at the beginning of the game, it’s anyone’s pick)
P(ShowGoat|OtherDoor) = 1, (100%, the host has only this option as the other door has the car)
P(OtherDoor) = 0.33 (original chance of the other door having a car)
P(ShowGoat|MyDoor) = (0.5 x 0.33) / [ (0.5 x 0.33) + (1 x 0.33)] = 0.33 (1 in 3 chance)
Now, evaluate the chances that the other door has the car once the host showed me a ‘goat door’. P(OtherDoor|ShowGoat) =
P(ShowGoat|OtherDoor) x P(OtherDoor) / [ P(ShowGoat|OtherDoor) x P(OtherDoor) + P(ShowGoat|MyDoor) x P(MyDoor)]
P(ShowGoat|OtherDoor) = chance of the host showing goat in that room if the other room has a car = 1 (or 100%, she has no other option)
P(OtherDoor) = prior chance of the other room having a car = 0.33 (or 1 in 3 at the beginning of the game)
P(ShowGoat|MyDoor) = 0.5. If my door has the car, the host had a 50% chance of opening that door
P(MyDoor) = 0.33 (my original chance of choosing one door)
P(OtherDoor|ShowGoat) = (1 x 0.33) / [ (1 x 0.33) + (0.5 x 0.33)] = 0.667 (2 in 3 chances)
So, switching doors has double the chance of winning than sticking to the original choice.
Method 2: Argument
In the beginning, you have a 1 in 3 chance of picking a door that has the car. That automatically means a 2 in 3 (67%) chance to find the car outside your door. Initially, that 67% was hiding behind two doors, but the host has helped you narrow that chance by removing one. It’s so simple!
Method 3: Perform Experiments
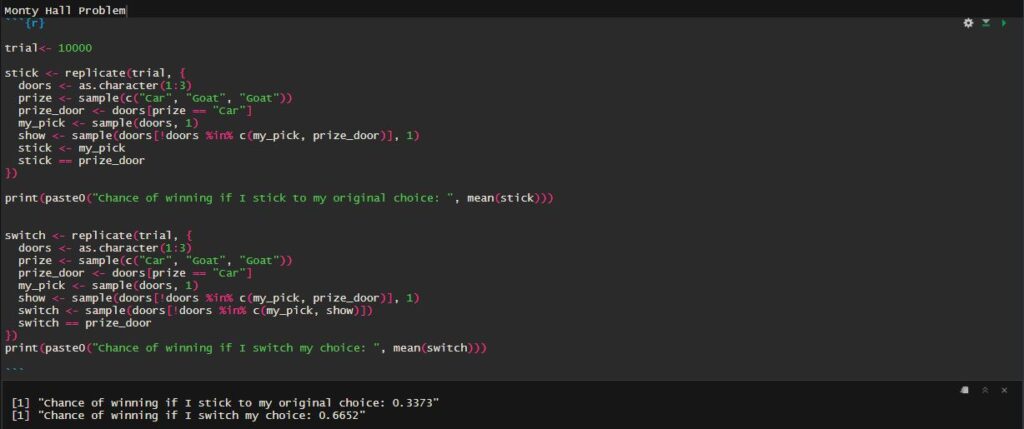
Still not convinced? Then, you do the actual experiment. There are two ways to experiment: 1) Build three doors, perform hundreds of trials with a partner, and find the average. 2) Perform a Monte Carlo simulation and run the trial a few thousand times. Trust me, I have done the latter using R programming, and the code is here: