Let’s play this game: game A) You lose a dollar every time you play one game; game B) you lose five dollars if the money at hand is odd and gain three dollars if it’s even. You have 100 bucks at the start of each game; play for 100 games.
Following are the first few results from game A, followed by the plot of the results.
| # | Money at hand |
| start | 100 |
| 1 | 99 |
| 2 | 98 |
| 3 | 97 |
| … | … |
| 100 | 0 |
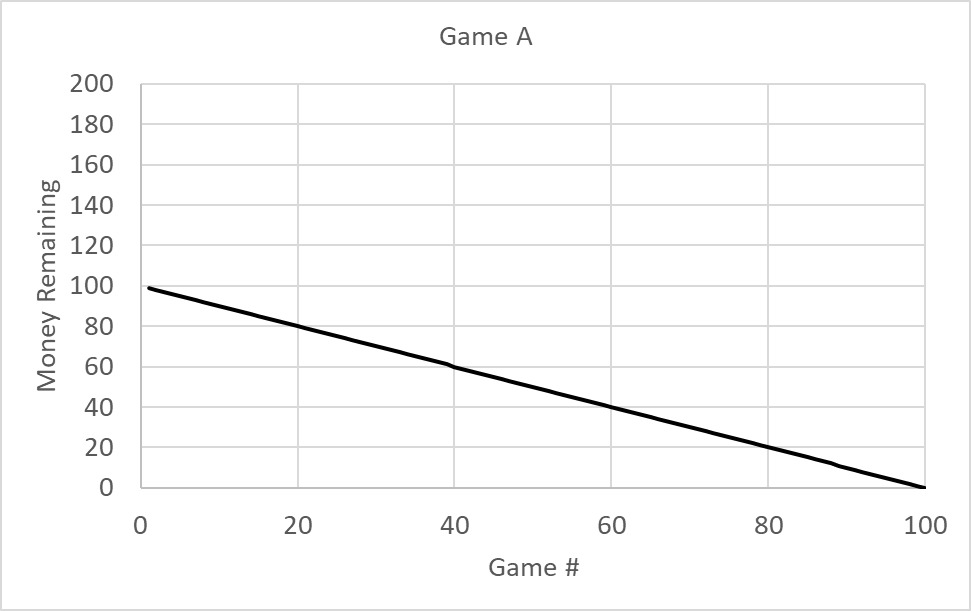
So, you are losing everything in 100 plays. Now, the second game: The excel code is: if(isodd(B1), B1-5, B1+3); assuming the starting 100 is in the cell, B1.
| # | Money at hand |
| start | 100 |
| 1 | 103 |
| 2 | 98 |
| 3 | 101 |
| 4 | 96 |
| … | … |
| 100 | 0 |
Again, you lose everything in 100.
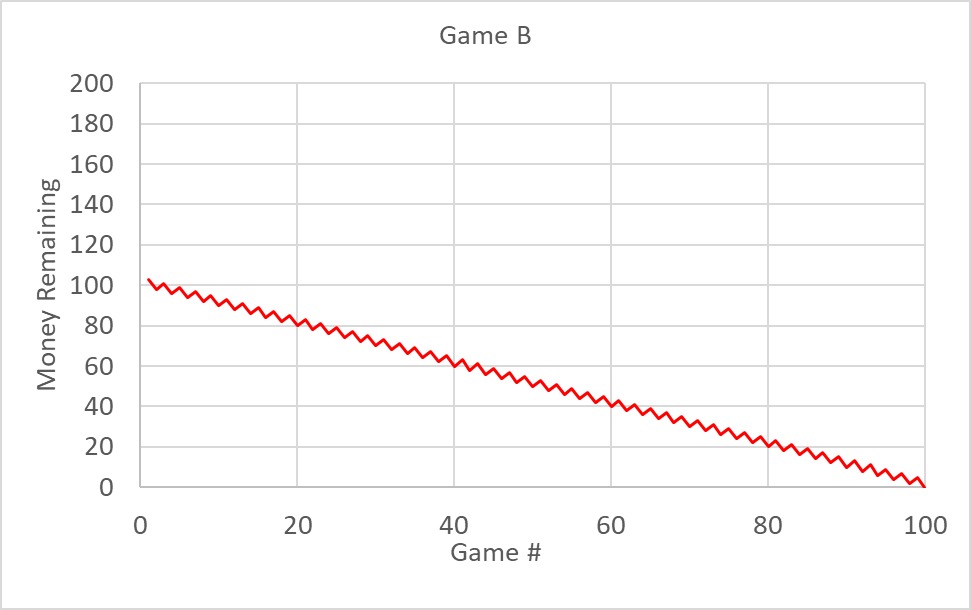
Play two losing games!
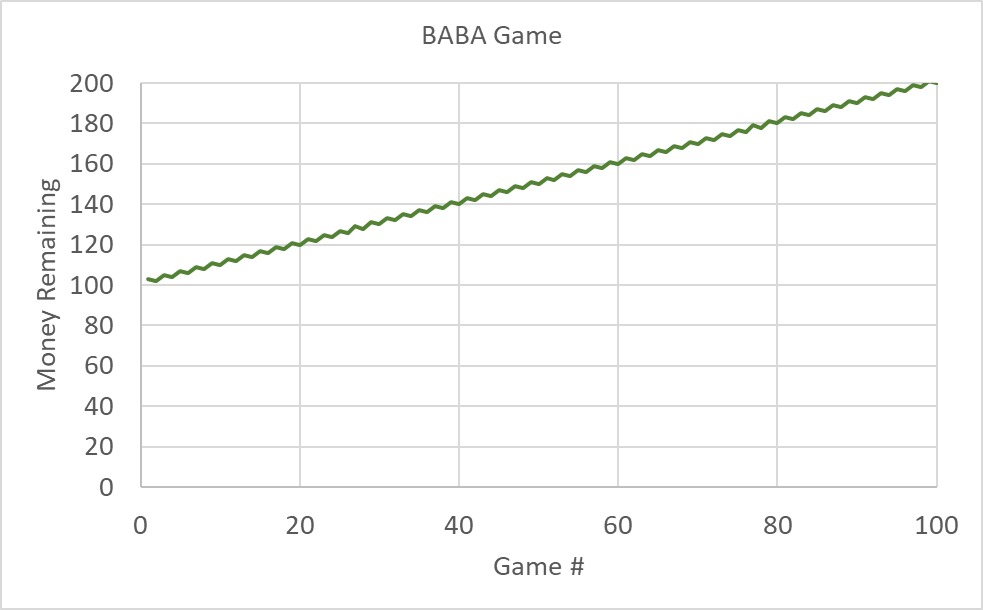
We have played two losing games. Now play game B and game A alternatively and see what happens. if(isodd(A2), if(isodd(B1), B1-5, B1+3), B1-1). The game number is in the A column, starting from A2, and money is in the B column, starting from B1.
| # | Money at hand |
| start | 100 |
| 1 | 103 |
| 2 | 102 |
| 3 | 105 |
| 4 | 104 |
| … | … |
| 100 | 200 |
Putting the outcomes of all three games in one place (back represents game A, red represents game B, and the green represents BABA game:
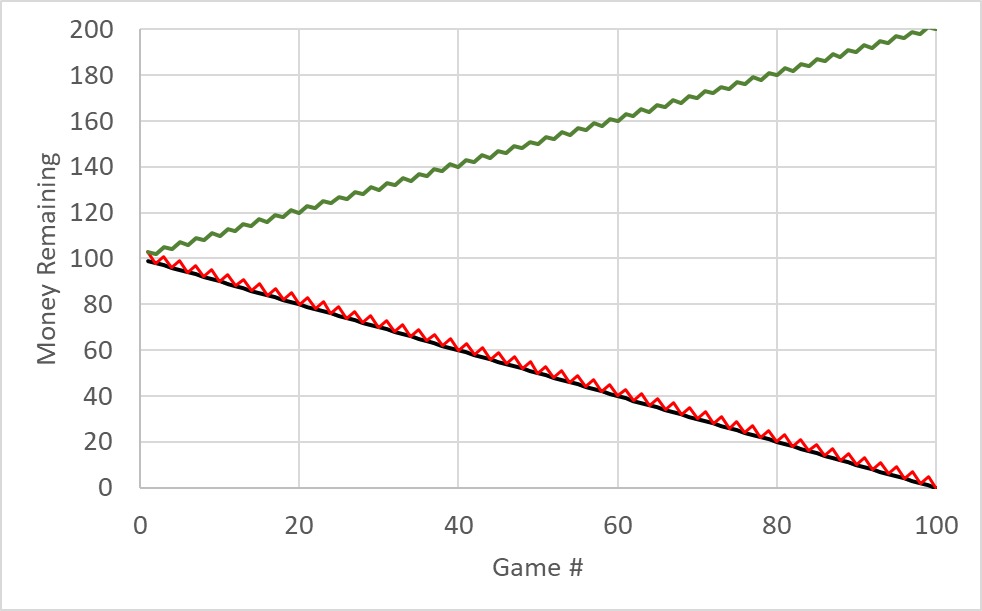
Where is the paradox?
An important thing to notice here is that game A influences game B (and evades the number from being odd before game B starts). The end result becomes counterintuitive, but not a paradox in the strictest sense.
Parrondo’s paradox: Wiki
The Game You Win By Losing (Parrondo’s Paradox): Vsauce2

