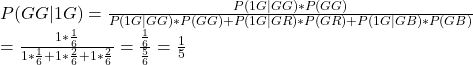Probability of Green Balls

There are four balls in a bowl – one red, one blue and two green. If one randomly takes out two balls and claims that at least one ball is green, what is the probability that both balls are green? We will use Bayes’ rule here but first, the prior probabilities.

The total number of pairs from four balls is ₄C₂ = 6. The prior chance of drawing two greens is 1 in 6, green with red is 2 in 6, and green with blue is also 2 in 6.

Let P(GG|1G) be the required probability of green-green, given at least one green,

$\\ P(GG|1G) = \frac{P(1G|GG)*P(GG)}{P(1G|GG)*P(GG) + P(1G|GR)*P(GR) + P(1G|GB)*P(GB)} \\ = \frac{1*\frac{1}{6}}{1*\frac{1}{6} + 1*\frac{2}{6} + 1*\frac{2}{6} } = \frac{\frac{1}{6}}{\frac{5}{6}} = \frac{1}{5}$

Related Posts