Probability of Cheat Coin

Anne has a bag with ten coins; one of them is a cheat coin (both side-heads). She picks up one coin and tosses it two times, and both are heads. What is the probability that she picked the cheat coin?

We all know that the probability of drawing the cheat coin from the bag is 1/10, but that was not the question here. It is on chance, given a piece of information is already available. So the ask must be an updated (Bayesian) guess. We can solve the problem in two ways.

Method 1: In one step

\\ P(CC|2H) = \frac{P(2H|CC)*P(CC)}{P(2H|CC)*P(CC) + P(2H|GC)*P(GC)} \\ \\ P(CC|2H) = \frac{1 * 1/10}{1 *(1/10) + (1/4)*(9/10)} = \frac{4}{13} = 0.31

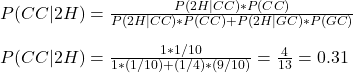
Method 2: Posterior as the new prior

\\ P(CC|H) = \frac{P(H|CC)*P(CC)}{P(H|CC)*P(CC) + P(H|GC)*P(GC)} \\ \\ P(CC|H) = \frac{1 * 1/10}{1 *(1/10) + (1/2)*(9/10)} = \frac{2}{11} \\ \\ P(CC|2H) = \frac{P(H|CC)*P(CC|H)}{P(H|CC)*P(CC|H) + P(H|GC)*(1-P(CC|H))} \\ \\ P(CC|2H) = \frac{1 * 2/11}{1 *(2/11) + (1/2)*(9/11)} = \frac{2}{13/2} = \frac{4}{13} = 0.31

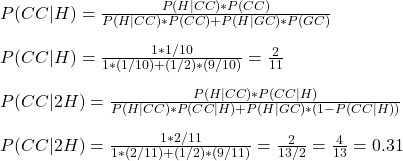
The notations are:
P(CC|2H) = chance that it is a cheat coin, given two times heads
P(2H|CC) = chance of two heads for a cheat coin
P(CC) = the prior chance for a cheat coin
P(2H|GC) = chance of two heads for a good coin
P(GC) = the prior chance for a good coin= 1 – P(CC)
P(CC|H) = chance that it is a cheat coin, given heads in the first toss
P(H|CC) = chance of heads for a cheat coin
P(H|GC) = chance of heads for a good coin

Related Posts