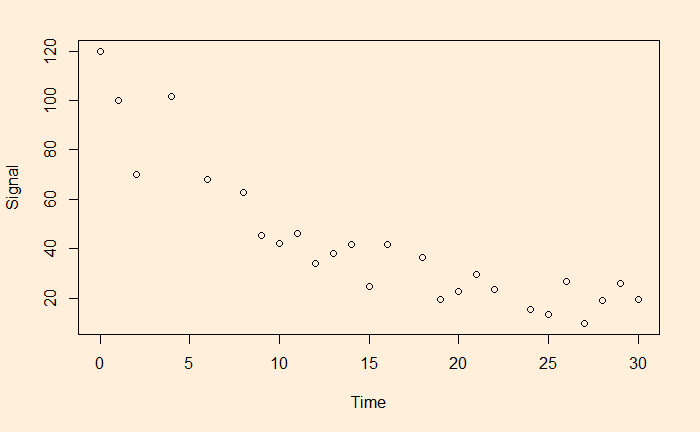
We have seen linear and non-linear regressions in the past. One type of non-linear function is exponential. A familiar example is the decay of a signal with time.
The easy way to perform the curve-fitting is to convert the exponential function to linear and perform an ordinary least square (OLS).
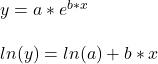
This is a linear function with slope = b and intercept = ln(a).
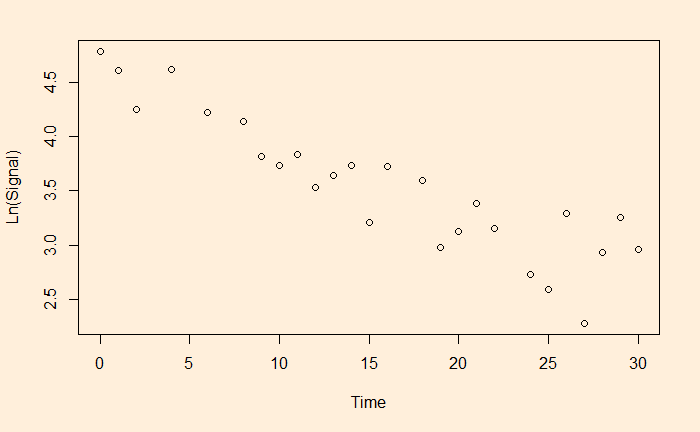
Let’s run a regression with these transformed variables.
df$ln <- log(df$Signal)
fit <- lm(ln ~ Time, data=df)
summary(fit)Gives the output as
Call:
lm(formula = ln ~ Time, data = df)
Residuals:
Min 1Q Median 3Q Max
-0.55119 -0.17134 0.03271 0.19116 0.54713
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.540757 0.110923 40.94 < 2e-16 ***
Time -0.063229 0.006115 -10.34 2.55e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2795 on 24 degrees of freedom
Multiple R-squared: 0.8167, Adjusted R-squared: 0.809
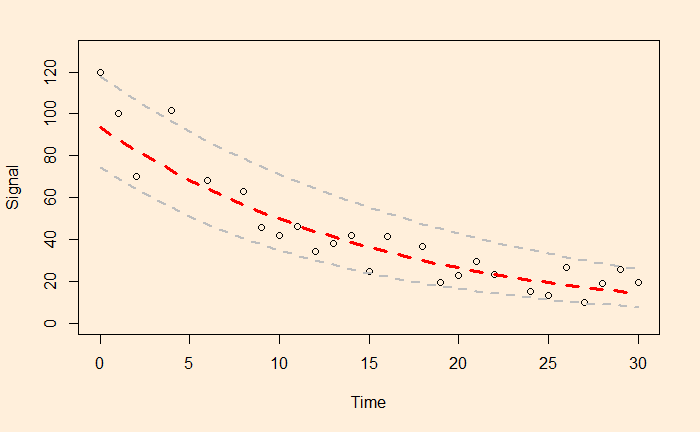
F-statistic: 106.9 on 1 and 24 DF, p-value: 2.552e-10a = e4.540757 and b = -0.063229 and here is the plot of data along with the fitted curve.
xx <- seq(0,30)
plot(df$Time, df$Signal, xlim = c(0,30), ylim = c(0,130), xlab = "Time", ylab = "Signal")
lines(xx, exp(fit$coefficients[1])*exp(fit$coefficients[2]*xx), col = "red", lty = 2, lwd = 3)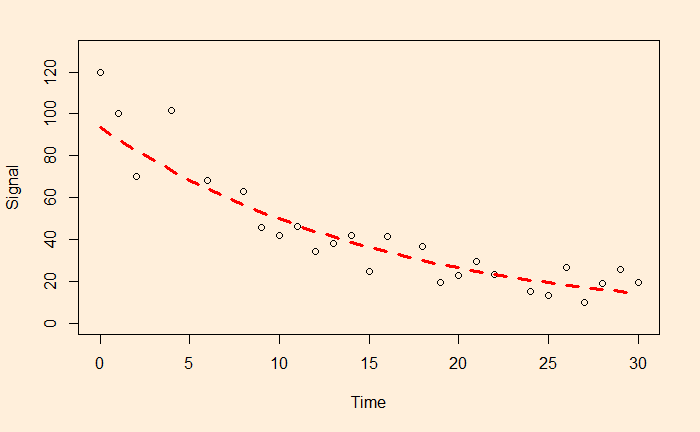
The next step is to get the confidence interval by running the confint() function.
conf_int <- confint(fit, level=0.95)
2.5 % 97.5 %
(Intercept) 4.31182187 4.76969119
Time -0.07585068 -0.05060753Incorporate them into the plot, and you get
xx <- seq(0,30)
plot(df$Time, df$Signal, xlim = c(0,30), ylim = c(0,130), xlab = "Time", ylab = "Signal")
lines(xx, exp(fit$coefficients[1])*exp(fit$coefficients[2]*xx), col = "red", lty = 2, lwd = 3)
lines(xx, exp(conf_int[1])*exp(conf_int[2]*xx), col = "grey", lty = 2, lwd = 2)
lines(xx, exp(conf_int[3])*exp(conf_int[4]*xx), col = "grey", lty = 2, lwd = 2)