We are back in the game of chances, the roulette – not the Vegas one, but the Russian. Imagine two rounds are put in a revolver that has six cartridges. You don’t know the order in which they are kept, i.e. next to each other, or there are gaps between them. What is the probability you get hit by the bullet?
It is pretty straightforward: there are two in six chances to get hit (2/6 = 33.3%), and four in six you survive (4/6 = 66.7%). OK, you survive the first round. If there is a second round and you have two choices. Pull the trigger straight away, or spin it again before pulling. Which one do you choose?
3 types of arrangements
The number of arrangements possible for two bullets to be placed inside six possible cartridges is 6C2 = 6!/(4!2!) = 6 x 5 / 1 x 2 = 15. Those 15 fall into three categories as below:
Next to each other
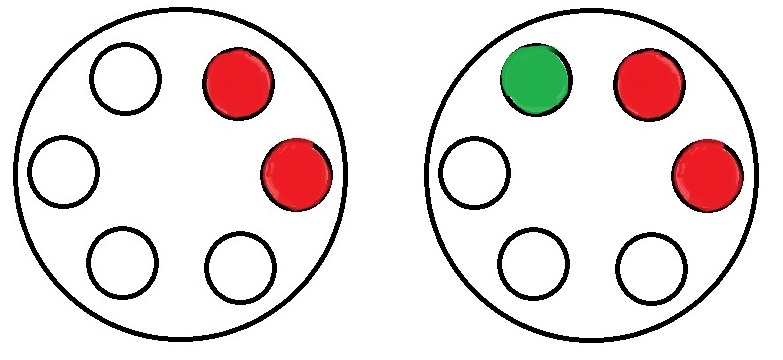
There are six such arrangements that are possible ({1,2}, {{2,3}, {3,4}, {4,5}, {5,6}, {6,1}). In the above figure, the left one with two reds represents one such. In such an arrangement, the number of empty spots that follows a bullet is just one (marked as green on the above right). Since there are four empty cartridges, the probability of the second one hitting is (1/4).
With one gap

Six arrangements are possible with one gap between them ({1,3}, {{2,4}, {3,5}, {4,6}, {5,1}, {6,2}). The chance of the second one hitting, in this case, is (2/4).
With two gaps

Three are are possible with two gaps between them ({1,4}, {{2,5}, {3,6}). The chance of hitting is again (2/4).
To spin or not to spin?
So what is the probability of surviving if you prefer to spin again? That will be the same as the first time = 66.7%. If not, you calculate the chances in the following manner.
6/15 (probability to get arrangements of type 1) x 3/4 (chance of survival) + 6/15 (probability to get arrangements of type 2) x 2/4 (chance of survival) + 3/15 (probability to get arrangements of type 3) x 2/4 (chance of survival) = 6/15 x 3/4 + 6/15 x 2/4 + 3/15 x 2/4 = (9/2 + 6/2 + 3/2)/15 = 9/15 = 0.6 = 60%.
The bottom line is: you better ask to spin again and increase the probability of survival by 6.7%!

