Managing Staff for Stochastic Births

Continuing with the Poisson distribution, we will work out an example today. The nursing supervisor of a busy hospital knows that, on average, 16 child-births happen in an 8-hr shift. How will she manage the wards, making sure the delivery service is optimally staffed?

Assuming delivery is dominated by natural delivery, which is stochastic, we resort to Poisson distribution to make the required calculations. Start with the extreme values.

What is the probability of having zero childbirth in a shift?

$\\ P(X = s) = \frac{e^{-\lambda}\lambda^s}{s!} \\ \\ \text {For zero births, s = 0. And we know } \lambda = 16. \\\\ P(X = 0) = \frac{e^{-16}*1}{1} = 0.0000001125$

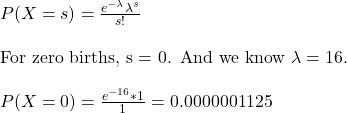
This can also be obtained directly using the R, ppois(0,16). What is the probability of getting up to 7 births (0 – 7)? ppois(7,16) = 0.00999 or about 1%. Also, the supervisor now knows at 90% certainty that it would not be more than 21 as ppois(21,16) is 91%.

Reference

Biostatistics for Medical and Biomedical Practitioners, 2015, Pages 259-278: Chapter 18 – The Poisson Distribution

Reference

Related Posts