Return of the Dice

What is the probability of rolling a dice six times and getting different faces?

dice, roll the dice, to play-2031512.jpg

Remember the conjunction rule (generalised AND rule) that connected the joint probability with the conditional probability?

P(A \displaystyle \cap B)= P(A) * P(B | A)

Back to dice

Let P(A1) be the probability of getting the first face = 1
P(A2|A1) be the probability of getting a different face from die 1 = (5/6)
P(A3|A1A2) be the probability of getting a different face from die 1 and die 2 = (4/6) etc.

We must find the joint probability of A1, A2, A3, A4, A5, and A6.

\\ P(A1 \displaystyle \cap A2 \displaystyle \cap A3 \displaystyle \cap A4 \displaystyle \cap A5 \displaystyle \cap A6)= P(A1) * P(A2 | A1) * P(A3 | A1A2) * P(A4 | A1A2A3) * P(A5 | A1A2A3A4)*P(A6 | A1A2A3A4A5) \\ \\ P(\text{all different)} = 1*\frac{5}{6}*\frac{4}{6}*\frac{3}{6}*\frac{2}{6}*\frac{1}{6} = \frac{5}{324} = 1.5 \%

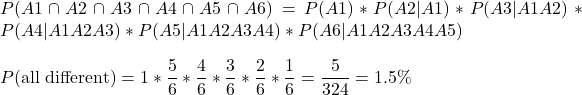
Frequentist way

For the first roll, there are six choices. Once the first slot is taken, there are five choices for the second roll. Therefore, 6 x 5 for the first and second choices together. If you extend the logic for all the six rolls, you get 6 x 5 x 4 x 3 x 2 x 1 or 6!

Possibilities for the required event = 6! = 720
Total possibilities of rolling six dice = 66 = 46656
P(for the required event) = 720/46656 = 1.5%

Related Posts